【题目】一个不透明的布袋里装有4个大小、质地都相同的乒乓球，球面上分别标有数字1，2，3，4，小明先从布袋中随机摸出一个乒乓球，不放回去，再从剩下的3个球中随机摸出第二个乒乓球．
（1）求小明第一次摸出的乒乓球所标数字是偶数的概率；
（2）请用树状图或列表的方法求两次摸出的乒乓球球面上数字的积为偶数的概率．
优加精卷系列答案科目：初中数学 来源： 题型：
【题目】如图，为了测量出楼房AC的高度，从距离楼底C处
米的点D（点D与楼底C在同一水平面上）出发，沿斜面坡度为i=1：
的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53°，求楼房AC的高度（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈
，计算结果用根号表示，不取近似值）．
查看答案和解析>>
科目：初中数学 来源： 题型：
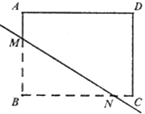
【题目】如图，已知矩形ABCD中，AB=6，AD=8将矩形ABCD沿直线MN翻折后，点B恰好落在边AD上的点E处，如果AE=2AM，那么CN的长为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市销售一种商品，成本每千克40元，规定每千克售价不低于成本，且不高于80元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 50 | 60 | 70 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），则当售价x定为多少元时，厂商每天能获得最大利润？最大利润是多少？
（3）如果超市要获得每天不低于1350元的利润，且符合超市自己的规定，那么该商品每千克售价的取值范围是多少？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB=
，AD=1．
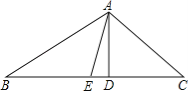
（1）求BC的长；
（2）求tan∠DAE的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
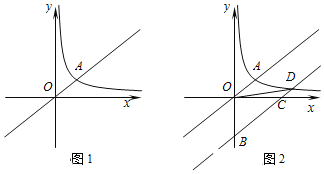
【题目】如图1，正比例函数y＝kx的图象与反比例函数y＝
（x＞0）的图象都经过点A（2，2）．
（1）分别求这两个函数的表达式；
（2）如图2，将直线OA向下平移n个单位长度后与y轴交于点B，与x轴交于点C，与反比例函数图象在第一象限内的交点为D，连接OD，tan∠COD＝
．
①求n的值．
②连接AB，AD，求△ABD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一张透明的平行四边形胶片沿对角线剪开，得到图①中的两张三角形胶片
和
．将这两张三角形胶片的顶点B与顶点E重合，把绕点B顺时针方向旋转，这时AC与DF相交于点O．
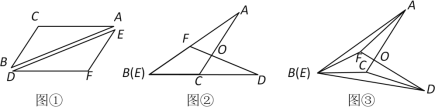
（1）当旋转至如图②位置，点B（E），C,D在同一直线上时，∠AFD与∠DCA的数量关系是 ．
（2）当继续旋转至如图③位置时，（1）中的结论还成立吗？请说明理由．
（3）在图③中，连接BO,AD，探索BO与AD之间有怎样的位置关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
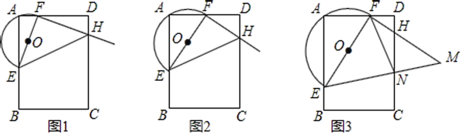
【题目】已知：在矩形ABCD中，E，F分别是边AB，AD上的点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O．
（1）填空：点A （填“在”或“不在”）⊙O上；当弦AE等于弦AF时，
的值是 ；
（2）如图1，在△EFH中，当FE＝FH时，求证：AD＝AE+DH；
（3）如图2，当△EFH的顶点F是边AD的中点时，求证：EH＝AE+DH；
（4）如图3，点M在线段FH的延长线上，若FM＝FE，连接EM交DC于点N，连接FN，当AE＝AD时，FN＝4，HN＝3，直接写出的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
