练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

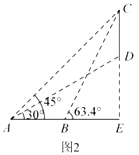
    【题目】某数学兴趣小组要测量实验大楼部分楼体的高度(如图1所示，部分)，在起点处测得大楼部分楼体的顶端点的仰角为45°，底端点的仰角为30°，在同一剖面沿水平地面向前走16米到达处，测得顶端的仰角为63.4°(如图2所示)，求大楼部分楼体的高度约为多少米？(精确到1米)(参考数据：，，，，)

    　　　　

    【答案】14（米）

    【解析】

    设楼高CE为x米，于是得到BE=x-16，然后再解直角三角形即可．

    解：设楼高CE为x米

    在Rt△AEC中，∠CAE=45°，

    ∴AE=CE=x ，AB=16

    ∴BE=x-16，

    在Rt△CEB中，CE= BE·tan63.4°≈2（x-16），

    ∴2（x-16）=x解得：x=32（米）

    在Rt△DAE中，DE= AE·tan30°=32×

    ∴CD=CE-DE=32-≈14（米）

    答：大楼部分楼体CD的高度约为14米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=x+4的图象与反比例函数y=（k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．

    （1）求此反比例函数的表达式；

    （2）若点P在x轴上，且S△ACP=S△BOC，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

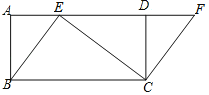
    【题目】如图，四边形ABCD是矩形，点E在AD边上，点F在AD的延长线上，且BE=CF．

    （1）求证：四边形EBCF是平行四边形．

    （2）若∠BEC=90°，∠ABE=30°，AB=，求ED的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论：①这个函数图象的顶点始终在直线y=-x+1上；②存在一个m的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；③点A(x1,y1)与点B(x2,y2)在函数图象上，若x1<x2，x1+x2>2m，则y1<y2；④当-1<x<2时，y随x的增大而增大，则m的取值范围为m≥2其中错误结论的序号是（ ）

    A. ①B. ②C. ③D. ④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

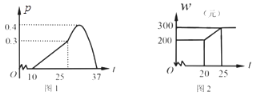
    【题目】某农作物的生长率P与温度t(℃)有如下关系：如图1，当10≤t≤25时可近似用函数刻画；当25≤t≤37时可近似用函数刻画．

    (1)求h的值．

    (2)按照经验，该作物提前上市的天数m(天)与生长率P满足函数关系：

    生长率P

    0.2

    0.25

    0.3

    0.35

    提前上市的天数m（天）

    0

    5

    10

    15

    ①请运用已学的知识，求m关于P的函数表达式；

    ②请用含的代数式表示m ；

    (3)天气寒冷，大棚加温可改变农作物生长速度．在(2)的条件下，原计划大棚恒温20℃时，每天的成本为200元，该作物30天后上市时，根据市场调查：每提前一天上市售出(一次售完)，销售额可增加600元．因此给大棚继续加温，加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2．问提前上市多少天时增加的利润最大？并求这个最大利润（农作物上市售出后大棚暂停使用）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】连接正八边形的三个顶点，得到如图所示的图形，下列说法错误的是（ ）

    A. 是等边三角形

    B. 连接，则分别平分和

    C. 整个图形是轴对称图形，但不是中心对称图形

    D. 四边形与四边形的面积相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

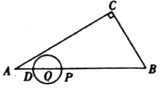
    【题目】如图，在中，，，，点在线段上，．点从点出发，沿方向运动，以为直径作，当运动到点时停止运动，设．

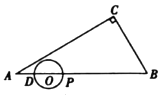
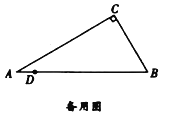
    （1）___________，___________．（用的代数式表示）

    （2）当为何值时，与的一边相切？

    （3）在点整个运动过程中，过点作的切线交折线于点，将线段绕点顺时针旋转得到，过作于．

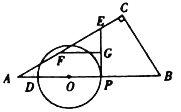
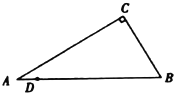
    ①当线段长度达到最大时，求的值；

    ②直接写出点所经过的路径长是________．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．

    （1）求m的值及C点坐标；

    （2）在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由；

    （3）P为抛物线上一点，它关于直线BC的对称点为Q．

    ①当四边形PBQC为菱形时，求点P的坐标；

    ②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

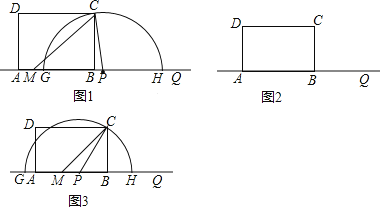
    【题目】如图，在矩形ABCD中，AB＝4，BC＝3．点M是AB边上一点，且∠CMB＝45°．点Q是直线AB上一点且在点B的右侧，BQ＝4，点P从点Q出发，沿射线QA方向以每秒2个单位长度的速度运动，设运动时间为t秒．以P为圆心，PC长为半径作半圆P，交直线AB分别于点G，H(点G在点H的左侧)．

    （1）当t＝1秒时，PC的长为　　　　，t＝　　　　秒时，半圆P与AD相切；

    （2）当点P与点B重合时，求半圆P被矩形ABCD的对角线AC所截得的弦长；

    （3）若∠MCP＝15°，请直接写出扇形HPC的弧长为 ．

    查看答案和解析>>

    同步练习册答案