
【题目】甲、乙两名同学进入初四后,某科6次考试成绩如图:
(1)请根据下图填写如表:
平均数 | 方差 | 中位数 | 众数 | 极差 | |
甲 | 75 | 75 | |||
乙 | 33.3 | 15 |
(2)请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行
①从平均数和方差相结合看;②从折线图上两名同学分数的走势上看,你认为反映出什么问题?

【答案】(1)125,75,35;75,72.5,70;(2)①从平均数和方差相结合看,乙同学成绩更稳定;②从折线图上两名同学分数的走势上看,甲同学进步较快,乙同学成绩稳定有小幅度下滑.
【解析】
试题(1)分别根据平均数、方差的求解进行计算,中位数的定义,众数的定义以及极差的定义解答;
(2)根据方差的意义以及折线统计图的意义解答.
试题解析:(1)甲:方差=![]() [(60-75)2+(65-75)2+(75-75)2+(75-75)2+(80-75)2+(95-75)2=
[(60-75)2+(65-75)2+(75-75)2+(75-75)2+(80-75)2+(95-75)2=![]() (225+100+0+0+25+400)=125,
(225+100+0+0+25+400)=125,
众数:75,
极差:95-60=35;
乙:平均数=![]() (85+70+70+75+70+80)=75,
(85+70+70+75+70+80)=75,
中位数:![]() (70+75)=72.5,
(70+75)=72.5,
众数:70;
(2)①从平均数和方差相结合看,乙同学成绩更稳定;
②从折线图上两名同学分数的走势上看,甲同学进步较快,乙同学成绩稳定有小幅度下滑.


科目:初中数学 来源: 题型:
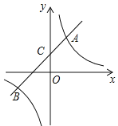
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点A(2,4)和点B(n,-2),与
的图像交于点A(2,4)和点B(n,-2),与![]() 轴交于点C.
轴交于点C.
(1)求m,n的值;
(2)当![]() 时,请直接写出
时,请直接写出![]() 的取值范围;
的取值范围;
(3)点B关于![]() 轴的对称点是B′,连接AB′,CB′,求△AB′C的面积.
轴的对称点是B′,连接AB′,CB′,求△AB′C的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
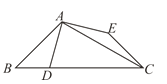
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游,不同租赁公司的租车费用(单位:元)与时间(单位:![]() )之间的关系如图所示.
)之间的关系如图所示.

根据以上信息,解答下列问题:
(1)设租车时间为![]() 时,租用甲公司的车所需费用为
时,租用甲公司的车所需费用为![]() 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为![]() 元,分别求出
元,分别求出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)请你帮助小明计算并选择哪个出游方案合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上运动,设
上运动,设![]() 长为
长为![]() ,
,![]() 的面积为
的面积为![]() .当
.当![]() 从小到大变化时,
从小到大变化时,![]() 也随之变化.
也随之变化.

(1)求出![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)完成下面的表格
| 4 | 5 | 6 | 7 |
| 6 |
(3)由表格看出当![]() 每增加
每增加![]() 时,
时,![]() 如何变化?
如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省攀枝花市)某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王周末骑电动车从家里出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离(米)与时间(分钟)之间的关系示意图,请根据图中提供的信息回答下列问题:
(1)在此变化过程中,自变量是 ,因变量是 .
(2)小王在新华书店停留了多长时间?
(3)买到书后,小王从新华书店到商场的骑车速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com