
分析 (1)求出最小的个整商系数即可.
(2)根据k($\frac{2}{a}$)>k($\frac{1}{a+1}$)分类讨论列出不等式解不等式即可.
(3)利用根与系数关系把k(x1)+k(x2)=9,转化为含有b的方程,记得分类讨论即可.
解答 解:(1)k($\frac{3}{2}$)=2,k(-$\frac{5}{2}$)=$\frac{6}{5}$.
故答案分别为2,$\frac{6}{5}$.
(2)∵k($\frac{2}{a}$)>k($\frac{1}{a+1}$),
当-1<a<0时,原式化为$-\frac{3}{2}a$>3(a+1)
∴a<-$\frac{2}{3}$,即-1<a<-$\frac{2}{3}$,
当a<-1时,原式化为$-\frac{3}{2}a$>-3(a+1)
解得a>-2,
故可知a的取值范围为-2<a<-1或-1<a<-$\frac{2}{3}$.
(3)设方程的两个根有x1<x2,
由于x1x2=$\frac{c}{a}=4$,故x1与x2同号.
当x2<0时,k(x1)+k(x2)=-$\frac{3}{{x}_{1}}-\frac{3}{{x}_{2}}$=-$\frac{3({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$=$\frac{3b}{4}=9$,
解得b=12.
当x1>0时,k(x1)+k(x2)=$\frac{3}{{x}_{1}}+\frac{3}{{x}_{2}}$=$\frac{3({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}}$=$\frac{-3b}{4}=9$,
解得b=-12.
综上b=±12.
点评 本题考查根与系数关系,解题的关键是理解题意,根据整商系数的定义解决问题,学会用转化的思想把问题转化为方程或不等式,题中也体现了分类讨论的数学思想.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:选择题
| A. | 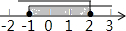 | B. |  | C. | 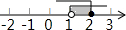 | D. | 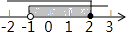 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
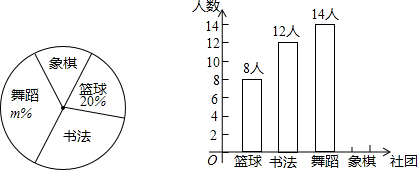
| 社团 | 篮球 | 书法 | 舞动 | 象棋 |
| 平均分 | 4 | 4.5 | 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com