
| ���� | ���� | �鷨 | �趯 | ���� |
| ƽ���� | 4 | 4.5 | 3 | 4 |
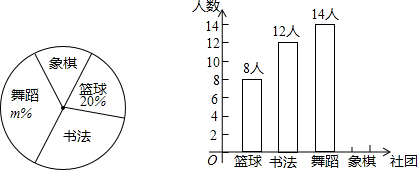
���� ��1���������ŵ�������8�ˣ���ռ����Ϊ20%������������������ٽ�һ���ó�����������������һ������赸��������ռ�������İٷֱ����m���ɣ�
��2�����ÿ�������ܷ֣���ӵó����������ܷ֣��ٳ������������ɣ�
��� �⣺��1��8��20%=40���ˣ���
40-8-12-14=6���ˣ���
14��40=35%
��ȫ����ͳ��ͼ���£�
��2����8��4+4.5��12+14��3+4��6���£�8+12+14+6��
=3.8���֣�
�𣺾ţ�1�������Ų�����ƽ����ʽ3.8�֣�
���� ���⿼���������ͳ��ͼ���ۺ����ã�����ͳ��ͼ����ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
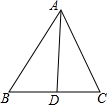 ��ͼ����ABC�У���BAC��ƽ����ΪAD����ADC=80�㣬��BAC�ȡ�B��10�㣬���ABC�������ڽǵĶ�����
��ͼ����ABC�У���BAC��ƽ����ΪAD����ADC=80�㣬��BAC�ȡ�B��10�㣬���ABC�������ڽǵĶ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
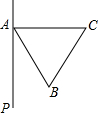 ��ͼ����֪�ȱߡ�ABC��ֱ��AP��
��ͼ����֪�ȱߡ�ABC��ֱ��AP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
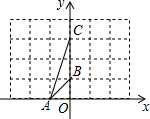 ��ͼ������A��B��C�����ABC����ֱ��AB�Գƣ����C�ĶԳƵ�C��������ǣ�2��1����
��ͼ������A��B��C�����ABC����ֱ��AB�Գƣ����C�ĶԳƵ�C��������ǣ�2��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
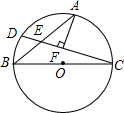 ��ͼ��BC�ǡ�O��ֱ������A��$\widehat{BC}$���е㣬DΪ$\widehat{AB}$��һ�㣬DC��AB��E��AF��CD��F��AF=2EF����֤��AE=BE��
��ͼ��BC�ǡ�O��ֱ������A��$\widehat{BC}$���е㣬DΪ$\widehat{AB}$��һ�㣬DC��AB��E��AF��CD��F��AF=2EF����֤��AE=BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com