
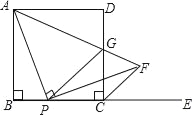
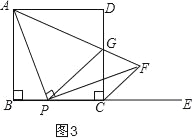
【题目】如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
猜想:线段PA与PF的数量关系为 .
探究:△CPG的周长在点P的运动中是否改变?若不改变求其值.
应用:若PG∥CF,当a=![]() 时,则PB= .
时,则PB= .
【答案】答案见解析.
【解析】试题分析:
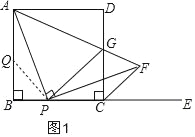
(1)猜想:PA=PF,在在BA边上截取BQ=BP,连接PQ,如图1:
通过证:∠BAP=∠CPF,∠AQB=∠PCF,AQ=CP证得△AQP≌△PCF,即可得到PA=PF;
(2)△CPG的周长在点P的运动中不改变,是一个定值;理由如下:
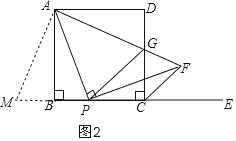
如图2,延长CB至M,使BM=DG,连接AM,先证△ABM≌△ADG,再证△PAM≌△PAG,从而可得:△CPG的周长= PG+PC+CG=PM+PC+CG=PB+BM+PC+CG
=PB+DG+PC+CG=BC+DC=2AB=2a;
(3)由PG∥CF可证得△PCG是等腰直角三角形,从而可得PC=GC,PG=![]() PC,设PB=
PC,设PB= ![]() ,则PC=GC=
,则PC=GC= ![]() ,PG=
,PG=![]() ;结合(2)中结论可得:
;结合(2)中结论可得: ![]() ,结合
,结合![]() 解此的方程,即可得到PB的值.
解此的方程,即可得到PB的值.
试题解析:
(1)猜想:PA=PF,理由是:
在BA边上截取BQ=BP,连接PQ,如图1:
可得△BPQ为等腰直角三角形,即∠BQP=45°,
∴∠AQP=135°,
又∵CF为直角∠DCE的平分线,
∴∠FCE=45°,
∴∠PCF=∠AQP=135°,
∵四边形ABCD为正方形,
∴∠B=∠BCD=∠D=90°,AB=BC=CD,
∴AB﹣BQ=BC﹣BP,即AQ=PC,
∵PF⊥AP,
∴∠APF=90°,
∴∠APB+∠CPF=90°,
又∵∠APB+∠QAP=90°,
∴∠QAP=∠CPF,
在△AQP和△PCF中, 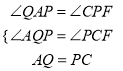 ,
,
∴△AQP≌△PCF(ASA),
∴PA=FP;
故答案为:PA=PF;
探究:△CPG的周长在点P的运动中不改变,是一个定值;
如图2,延长CB至M,使BM=DG,连接AM,
∵AD=AB,∠ABM=∠ADG=90°,
∴△ABM≌△ADG,
∴∠GAD=∠BAM,AG=AM,
由(1)可得得:AP=PF,又∵AP⊥PF,
∴△APF是等腰直角三角形,
∴∠PAG=45°,
∵∠BAD=90°,
∴∠GAD+∠BAP=45°,
∴∠BAM+∠BAP=45°,
∴∠MAP=∠PAG=45°,
又∵AP=AP,
∴△PAM≌△PAG,
∴PM=PG,
∴△PCG的周长=PG+PC+CG,
=PM+PC+CG,
=PB+BM+PC+CG,
=PB+DG+PC+CG,
=BC+DC,
=2a;
应用:如图3,∵PG∥CF,
∴∠PGC=∠GCF=45°,
∴△PCG是等腰直角三角形,
∴PC=CG,
设PB=x,则PC=CG=a﹣x,
由探究得:△PCG的周长=2a,
则PG+PC+CG=2a,
![]() PC+2PC=2a,
PC+2PC=2a,
![]() (a﹣x)=2a,
(a﹣x)=2a,
把![]() 代入得:
代入得: 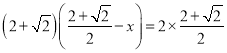
解得: ![]() ,即PB=
,即PB=![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.

查看答案和解析>>
科目:初中数学 来源: 题型:
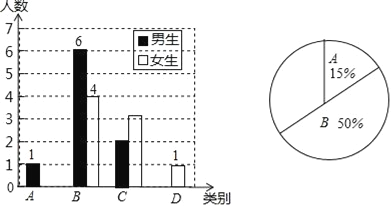
【题目】课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2006次后,点B所对应的数是( )
![]()
A、2005 B、2006 C、2007 D、2008
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.结合阅读材料,完成下列问题:
(1)下列哪个四边形一定是和谐四边形 .
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
(2)命题:“和谐四边形一定是轴对称图形”是 命题(填“真”或“假”).
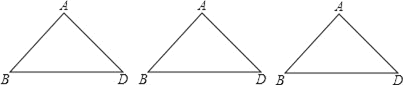
(3)如图,等腰Rt△ABD中,∠BAD=90°.若点C为平面上一点,AC为凸四边形ABCD的和谐线,且AB=BC,请求出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
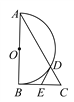
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小明想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离,于是小明在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°,已知公寓楼AD的高为60米,请你帮助小明计算出大厦的高度BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片的烂泥湿地,为了人员和设备安全迅速地通过这片湿地,他们沿着前进路线铺了若干块大小不同的木板,构筑成一条临时通道,已知当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
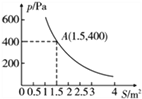
(1)请直接写出p与S 之间的关系式和自变量S 的取值范围;
(2)当木板面积为0.2 m2时,压强是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com