
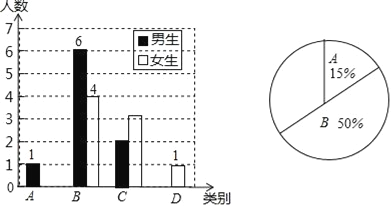
����Ŀ����ǰԤϰ��ѧϰ����Ҫ���ڣ�Ϊ���˽����̰༶ѧ����ɿ�ǰԤϰ�ľ��������ij�����ζԱ��ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��飬������������Ϊ���ࣺA�����㣬B�����ã�C��һ�㣬D���ϲ�������������Ƴ�����������������ͳ��ͼ��
��1�����ε������������������������A��Ů������������D��ѧ������������
��2��������ͳ��ͼ������ͳ��ͼ����������
��3�����ӱ������A���D��ѧ���и����ѡȡһλѧ�����С�һ��һ������ѧϰ����A��ѧ������D��ѧ���������б�������״ͼ�ķ��������ѡ��λͬѧ��ǡ����һλŮͬѧ����һλ��ͬѧ�ĸ��ʣ�
���𰸡���1��20��2��2����2��25%��10%����3��![]()
�������������������1������B����6+4=10�ˣ���ռ�ı�����50%���ݴ˼�������������������A���������ɵ�A��Ů���������ɸ��������֮��Ϊ�������ɵ�D��������
��2�����ã�1������õĽ������Ӧ����������������Ϊ��ٷֱȣ���ȫͼ�μ��ɵã�
��3�������оٷ����ɱ�ʾ�����������Ȼ�����ø��ʹ�ʽ������⣮
�����������1�����ε����ѧ����=��6+4����50%=20��������
��A��Ů���У�20��15%-1=2��������D��ѧ����20-��3+10+5��=2��������
�ʴ�Ϊ��20��2��2��
��2��C��ٷֱ�Ϊ![]() ��100%=25%��D���ٷֱ�Ϊ
��100%=25%��D���ٷֱ�Ϊ![]() ��100%=10%��
��100%=10%��
��ȫͼ�����£�
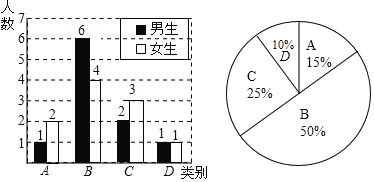
��3�������⻭����ͼ���£�
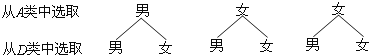
������ͼ���������п��ܳ��ֵĽ������6�֣���ÿ�ֽ�����ֵĿ�������ȣ���ѡһλŮͬѧ����һλ��ͬѧ�Ľ������2�֣�
����P��һλŮͬѧ����һλ��ͬѧ��=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ��ȤС���У�ͬѧ������һ�������ѵ���Ϸ��������ͬѧA��B��C��D��E��F�ֱ�������Ŵ�ֽ�Ƶĺ��棬��ͼ��A��B��C��D��E��F���ֵ�ֽ�Ƶ�ǰ��ֱ�д��������ʽ��66��63+63����63��3����2��62������3��63������22��32��3����64��3��62����Ϸ�涨��������ʽ��ֵ��ȵ������������ѣ����������ͬѧA�����������ѣ���������˭�أ�˵˵��Ŀ�����
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С������������Ϊ3��ֽ�������������һ�������ǽ�С�Ľ���Ϊ60�����������ص����ֵ����Ϊ______.
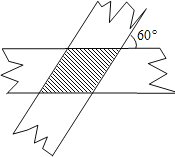
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ķ�����IJ��ϣ�����й����⣮
���ϣ���ѧϰ����ֵʱ����ʦ�̹����Ǿ���ֵ�ļ��κ��壬��![]() ��ʾ
��ʾ![]() ��
��![]() �������϶�Ӧ������֮��ľ��룻
�������϶�Ӧ������֮��ľ��룻![]() ������
������![]() ��ʾ
��ʾ![]() ��
��![]() �������϶�Ӧ������֮��ľ��룻
�������϶�Ӧ������֮��ľ��룻![]() ������
������![]() ��ʾ
��ʾ![]() �������϶�Ӧ�ĵ㵽ԭ��ľ��룮
�������϶�Ӧ�ĵ㵽ԭ��ľ��룮
һ��أ���![]() ����
����![]() �������Ϸֱ��ʾ������
�������Ϸֱ��ʾ������![]() ��
��![]() ����ô��
����ô��![]() ����
����![]() ֮��ľ���ɱ�ʾΪ
֮��ľ���ɱ�ʾΪ![]() ��
��
��1����![]() ��
��![]() ��
��![]() �������Ϸֱ��ʾ������
�������Ϸֱ��ʾ������![]() ��
��![]() ��
��![]() ����ô��
����ô��![]() ����
����![]() �ľ������
�ľ������![]() ����
����![]() �ľ���֮�Ϳɱ�ʾΪ__________���ú�����ֵ��ʽ�ӱ�ʾ����
�ľ���֮�Ϳɱ�ʾΪ__________���ú�����ֵ��ʽ�ӱ�ʾ����
��2����������̽����
������![]() ��
��![]() ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��
������![]() ��
��![]() ������ֵ��__________��
������ֵ��__________��
����![]() ����
����![]() ��ֵȡ�ڲ�С��
��ֵȡ�ڲ�С��![]() �Ҳ�����
�Ҳ�����![]() �ķ�Χʱ��
�ķ�Χʱ��![]() ��ֵ�Dz���ģ�������
��ֵ�Dz���ģ�������![]() ����Сֵ�������Сֵ��_____��
����Сֵ�������Сֵ��_____��
��3����չ��
��![]() ����СֵΪ__________��
����СֵΪ__________��
��![]() ����СֵΪ__________��
����СֵΪ__________��
��![]() ����СֵΪ__________����ʱ
����СֵΪ__________����ʱ![]() ��ȡֵ��ΧΪ__________��
��ȡֵ��ΧΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���������C1��y=x2�Ƶ㣨1��0����ת180���õ�������C2������������C1��C2��λ�ک�2��x��2��Χ�ڵIJ���Ϊͼ��C3����һ�κ���y=kx+k��1��k��0����ͼ����ͼ��C3���������㣬��k�ķ�Χ�ǣ�__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������м���ԭ��360ǧ�ˣ�����ԭ��290ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ��50������֪����һ��A�ֲ�Ʒ�ü���ԭ��9ǧ�ˣ�����ԭ��3ǧ�ˣ��ɻ���700Ԫ������һ��B�ֲ�Ʒ�ü���ԭ��4ǧ�ˣ�����ԭ��10ǧ�ˣ��ɻ���1200Ԫ��
��1����Ҫ����A��B���ֲ�Ʒ���������������ļ��ַ�����������Ƴ�����
��2��������A��B���ֲ�Ʒ������ΪyԪ������һ�ֲ�Ʒ��������Ϊx������д��y��x֮��ĺ�����ϵʽ�������ú���������˵�����ַ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90������B=30��������ABC�Ƶ�C��˳ʱ�뷽����תn�Ⱥõ���DEC����D�պ�����AB���ϣ�

��1����n��ֵ��
��2����F��DE���е㣬�ж��ı���ACFD����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AB=a��PΪ��BC��һ���㣨����B��C�غϣ���E�DZ�BC�ӳ�����һ�㣬����AP������P��PF��AP����DCE��ƽ�����ڵ�F������AF���CD���ڵ�G������PG��
���룺�߶�PA��PF��������ϵΪ�� ����
̽������CPG���ܳ��ڵ�P���˶����Ƿ�ı䣿�����ı�����ֵ��
Ӧ�ã���PG��CF����a=![]() ʱ����PB=�� ����
ʱ����PB=�� ����
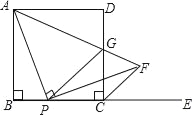
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��Ϊ
��Ϊ![]() �ϵĵ㣬
�ϵĵ㣬![]() Ϊ
Ϊ![]() �ϵĵ㣬
�ϵĵ㣬![]() ��
��![]() ����ô
����ô![]() ��
��

�����������������.
��![]() ��
��
![]() .��______��
.��______��
��![]() ��______��
��______��
��______![]() ______����______��
______����______��
��![]() ��______��
��______��
��![]() ��
��
��![]() ��______��.
��______��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com