
【题目】如图,![]() 点为
点为![]() 上的点,
上的点,![]() 为
为![]() 上的点,
上的点,![]() ,
,![]() ,那么
,那么![]() ,
,

请完成它成立的理由.
∵![]() ,
,
![]() .(______)
.(______)
∴![]() (______)
(______)
∴______![]() ______,(______)
______,(______)
∴![]() (______)
(______)
∵![]() ,
,
∴![]() (______).
(______).
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
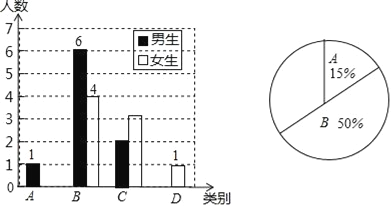
【题目】课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
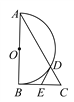
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小明想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离,于是小明在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°,已知公寓楼AD的高为60米,请你帮助小明计算出大厦的高度BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() ,将线段
,将线段![]() 平移至
平移至![]() ,点
,点![]() 在
在![]() 轴正半轴上(不与点
轴正半轴上(不与点![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
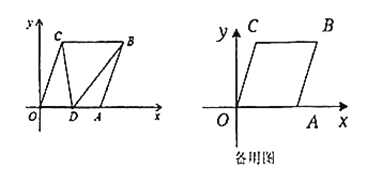
(1)写出点![]() 的坐标;
的坐标;
(2)当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标;
的坐标;
(3)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 、
、![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.

(1)求证:四边形BFDE是菱形;
(2)若ED=5,BD=8,求菱形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价80元,乙种每件进价60元,计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?
(2)服装店在销售中发现:甲服装平均每天可售出20件,每件盈利40元.经市场调查发现:如果每件甲服装降价4元,那么平均每天就可多售出8件,要想平均每天销售甲服装上盈利1200元,那么每件甲服装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片的烂泥湿地,为了人员和设备安全迅速地通过这片湿地,他们沿着前进路线铺了若干块大小不同的木板,构筑成一条临时通道,已知当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
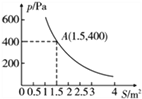
(1)请直接写出p与S 之间的关系式和自变量S 的取值范围;
(2)当木板面积为0.2 m2时,压强是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() .
.

(1)如图1,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .若
.若![]() ,求线段
,求线段![]() 的长.
的长.
(2)如图2,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),以
重合),以![]() 为边向上构造等边三角形
为边向上构造等边三角形![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.连接
的中点.连接![]() ,
,![]() 判断
判断![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
(3)在(2)的条件下,若![]() ,请你直接写出
,请你直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com