
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.
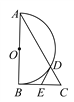
(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
【答案】(1)证明见解析;(2) AD=6.
【解析】试题分析:(1)连接OD,OE,由AB为圆的直径得到三角形BCD为直角三角形,再由E为斜边BC的中点,得到DE=BE=DC,再由OB=OD,OE为公共边,利用SSS得到三角形OBE与三角形ODE全等,由全等三角形的对应角相等得到DE与OD垂直,即可得证;
(2)在直角三角形ABC中,由∠BAC=30°,得到BC为AC的一半,根据BC=2DE求出BC的长,确定出AC的长,再由∠C=60°,DE=EC得到三角形EDC为等边三角形,可得出DC的长,由AC﹣CD即可求出AD的长.
试题解析:(1)连接OD,OE,BD,
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
OB=OD,OE=OE,BE=DE,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
则DE为圆O的切线;
(2)在Rt△ABC中,∠BAC=30°,
∴BC=![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6.


科目:初中数学 来源: 题型:
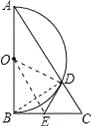
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
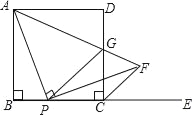
【题目】如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
猜想:线段PA与PF的数量关系为 .
探究:△CPG的周长在点P的运动中是否改变?若不改变求其值.
应用:若PG∥CF,当a=![]() 时,则PB= .
时,则PB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
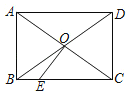
【题目】如图,矩形ABCD中,AD=4,对角线AC与BD交于点O,OE⊥AC交BC于点E,CE=3,则矩形ABCD的面积为( )
A.![]() B.
B.![]() C.12D.32
C.12D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若, ![]()
求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 | 1 | 2 | 3 | 4 | 5 | … |
电话费/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的关系式是什么?
(3)如果打电话超出![]() 分钟,需多付多少电话费?
分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是![]() 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点为
点为![]() 上的点,
上的点,![]() 为
为![]() 上的点,
上的点,![]() ,
,![]() ,那么
,那么![]() ,
,

请完成它成立的理由.
∵![]() ,
,
![]() .(______)
.(______)
∴![]() (______)
(______)
∴______![]() ______,(______)
______,(______)
∴![]() (______)
(______)
∵![]() ,
,
∴![]() (______).
(______).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com