
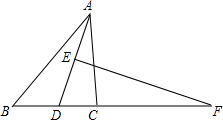
 如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC.
如图,在△ABC中,AD的垂直平分线交AD于E,交BC的延长线于F,FD2=FB•FC,求证:AD平分△BAC. 分析 连结FA,如图,根据线段垂直平分线性质得FA=FD,则利用等腰三角形的性质得∠EAF=∠EDF,由于FD2=FB•FC,则FA2=FB•FC,加上∠AFC=∠BFA,于是可判断△FAC∽△FBA,根据相似三角形的性质得∠FAC=∠B,接着利用三角形外角性质得∠EDF=∠B+∠BAD,所以∠CAD=∠BAD,于是可判断AD平分∠BAC.
解答 证明:如图,连接AF,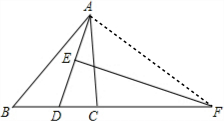
∵EF是AD的垂直平分线,
∴AF=DF,∠EAF=∠EDF,
∵FD2=FB•FC即$\frac{DF}{CF}=\frac{BF}{DF}$,
∴$\frac{AF}{CF}=\frac{BF}{AF}$,
∵∠AFC=∠BFA,
∴△AFC∽△BFA,
∴∠FAC=∠B,
∵∠EAF=∠EDF即∠FAC+∠CAD=∠BAD+∠B,
∴∠BAD=∠CAD,
即AD平分∠BAC.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时,只有运用对应角相等,对应边的比相等.也考查了线段垂直平分线的性质


科目:初中数学 来源: 题型:解答题
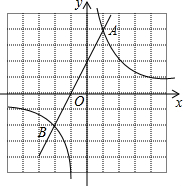 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
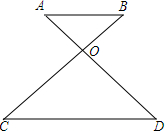 如图,OA:OD=OB:OC=1:2,OB=3.
如图,OA:OD=OB:OC=1:2,OB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
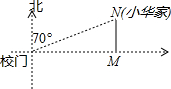 如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).
如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com