
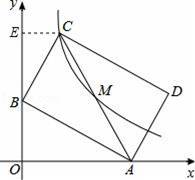
如图,已知:直线y=﹣
 x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=
x+1与坐标轴交于A,B两点,矩形ABCD对称中心为M,双曲线y=
 (x>0)正好经过C,M两点,则k= .
(x>0)正好经过C,M两点,则k= .
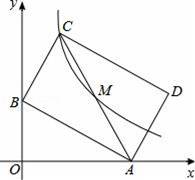

4 .
【考点】反比例函数综合题.
【分析】根据一次函数的解析式y=﹣
 x+1得到A(3,0),B(0,1),求得OA=3,OB=1,过C作CE⊥y轴于E,由四边形ABCD是矩形,得到∠CBA=90°,推出△BCE∽△ABO,得到比例式
x+1得到A(3,0),B(0,1),求得OA=3,OB=1,过C作CE⊥y轴于E,由四边形ABCD是矩形,得到∠CBA=90°,推出△BCE∽△ABO,得到比例式
 =
=
 ,设OC=x,则BE=3x,C(x,3x+1),由于矩形ABCD对称中心为M,得到M(x+
,设OC=x,则BE=3x,C(x,3x+1),由于矩形ABCD对称中心为M,得到M(x+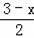
 ,
,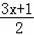
 ),根据反比例函数图象上点的坐标特征列方程x(3x+1)=(x+
),根据反比例函数图象上点的坐标特征列方程x(3x+1)=(x+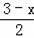
 )(
)(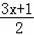
 ),解得x=1,求得C(1,4),即可得到结果.
),解得x=1,求得C(1,4),即可得到结果.
【解答】解:在y=﹣
 x+1中,令x=0,得y=1,令y=0,x=3,
x+1中,令x=0,得y=1,令y=0,x=3,
∴A(3,0),B(0,1),
∴OA=3,OB=1,
过C作CE⊥y轴于E,
∵四边形ABCD是矩形,
∴∠CBA=90°,
∴∠CBE+∠OBA=∠OBA+∠BAO=90°,
∴∠CBE=∠BAO,
∵∠BEC=∠AOB=90°,
∴△BCE∽△ABO,
∴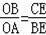
 =
=
 ,
,
设OC=x,则BE=3x,
∴C(x,3x+1),
∵矩形ABCD对称中心为M,
∴M(x+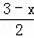
 ,
,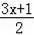
 ),
),
∵双曲线y=
 (x>0)正好经过C,M两点,
(x>0)正好经过C,M两点,
∴x(3x+1)=(x+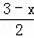
 )(
)(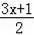
 ),
),
解得:x=1,
∴C(1,4),
∴k=1×4=4,
故答案为:4.

【点评】本题考查了矩形的性质,求直线与坐标轴的交点,相似三角形的判定和性质,反比例函数图象上点的坐标特征,作出辅助线构造相似三角形是解题的关键.


科目:初中数学 来源: 题型:
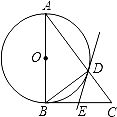
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与边AC交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)证明:DE是⊙O的切线;
(2)若⊙O的半径R=5,tanA=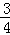 ,求线段CD的长.
,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )
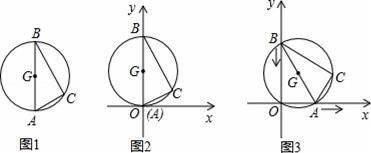

A.4 B.6 C.4
 ﹣2 D.10﹣4
﹣2 D.10﹣4

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),将△ABC绕原点O旋转180度得到△A1B1C1.结合所给的平面直角坐标系解答下列问题:
(1)画出△A1B1C1;
(2)画出一个△A2B2C2,使它分别与△ABC,△A1B1C1轴对轴(其中点A,B,C与点A2,B2,C2对应);
(3)在(2)的条件下,若过点B的直线平分四边形ACC2A2的面积,请直接写出该直线的函数解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为 .
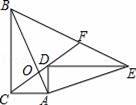

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=3,AD=4,动点E从B点沿BC边移动到C停止,DF⊥AE于F,设E在运动过程中,AE长为x,DF长为y,则下列能反映y与x函数关系的是( )


A.y=7x B.y=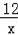
 C.y=
C.y=
 D.y=
D.y=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com