
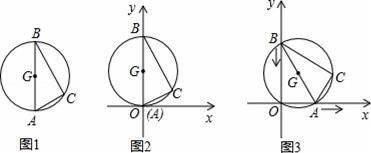
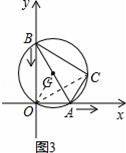
图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )

A.4 B.6 C.4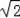
 ﹣2 D.10﹣4
﹣2 D.10﹣4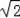

D
【考点】三角形的外接圆与外心;勾股定理;圆周角定理;弧长的计算.
【专题】压轴题;动点型.
【分析】由于在运动过程中,原点O始终在⊙G上,则弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,故点C在与x轴夹角为∠ABC的射线上运动.顶点C的运动轨迹应是一条线段,且点C移动到图中C2位置最远,然后又慢慢移动到C3结束,点C经过的路程应是线段C1C2+C2C3.
【解答】解:如图3,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO=
 AB=半径,
AB=半径,
∴原点O始终在⊙G上.
∵∠ACB=90°,AB=6,AC=2,∴BC=4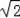
 .
.
连接OC.则∠AOC=∠ABC,∴tan∠AOC=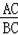
 =
=
 ,
,
∴点C在与x轴夹角为∠AOC的射线上运动.
如图4,C1C2=OC2﹣OC1=6﹣2=4;
如图5,C2C3=OC2﹣OC3=6﹣4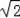
 ;
;
∴总路径为:C1C2+C2C3=4+6﹣4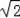
 =10﹣4
=10﹣4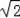
 .
.
故选:D.



【点评】主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
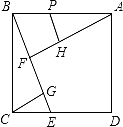
如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交A B于P.若CG=3.则△CGE与四边形BFHP的面积之和为 .
B于P.若CG=3.则△CGE与四边形BFHP的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
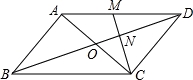
如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=
 x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)试写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入﹣购进成本.
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=x2﹣2x向右平移2个单位再向上平移3个单位,所得图象的解析式为( )
A.y=x2+3 B.y=x2﹣4x+3 C.y=x2﹣6x+11 D.y=x2﹣6x+8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com