
某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=
 x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
x+30(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)试写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入﹣购进成本.
【考点】二次函数的应用.
【专题】应用题;压轴题.
【分析】(1)运用营销问题中的基本等量关系:销售利润=日销售量×一件销售利润.一件销售利润=一件的销售价﹣一件的进价,建立函数关系式;
(2)分析函数关系式的类别及自变量取值范围求最大值;其中R1是二次函数,R2是一次函数.
【解答】解:(1)根据题意,得
R1=P(Q1﹣20)=(﹣2x+80)[(
 x+30)﹣20],
x+30)﹣20],
=﹣x2+20x+800(1≤x≤20,且x为整数),
R2=P(Q2﹣20)=(﹣2x+80)(45﹣20),
=﹣50x+2000(21≤x≤30,且x为整数);
(2)在1≤x≤20,且x为整数时,
∵R1=﹣(x﹣10)2+900,
∴当x=10时,R1的最大值为900,
在21≤x≤30,且x为整数时,
∵R2=﹣50x+2000,﹣50<0,R2随x的增大而减小,
∴当x=21时,R2的最大值为950,
∵950>900,
∴当x=21即在第21天时,日销售利润最大,最大值为950元.
【点评】本题需要反复读懂题意,根据营销问题中的基本等量关系建立函数关系式,根据时间段列出分段函数,再结合自变量取值范围分别求出两个函数的最大值,并进行比较,得出结论.


科目:初中数学 来源: 题型:
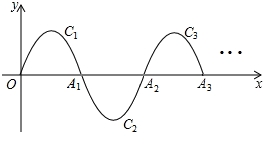
一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…若P是其中某段抛物线上一点,则m=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
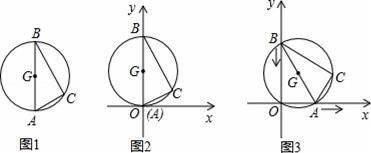
图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )

A.4 B.6 C.4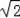
 ﹣2 D.10﹣4
﹣2 D.10﹣4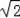

查看答案和解析>>
科目:初中数学 来源: 题型:
已知:一次函数y=kx+b中,当自变量x=3时,函数值y=5;当x=﹣4时,y=﹣9.
(1)求这个一次函数解析式;
(2)解关于x的不等式kx+b≤7的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两名自行车运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时乙在甲前10千米;④3小时时甲追上乙.其中正确的个数有( )


A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:直线y=﹣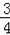
 x+3与x轴y轴分别交于点A、点B,抛物线y=﹣
x+3与x轴y轴分别交于点A、点B,抛物线y=﹣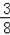
 x2+bx+c经过点A和点B.
x2+bx+c经过点A和点B.
(1)求抛物线的解析式;
(2)点C(0,2),点P(m,0)是线段OA上的一点(不与O、A重合),过点P作PM垂直x轴,交抛物线于点M,连接BM、AC、AM,设四边形ACBM的面积为S,求S与m的函数关系式(不要求写出自变量的取值范围);
(3)在(2)的条件下,点D是线段OP的中点,连接BD,当S取最大值时,试求直线BD与AC所成的锐角度数.
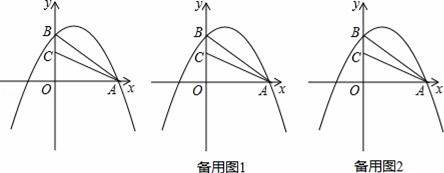

查看答案和解析>>
科目:初中数学 来源: 题型:
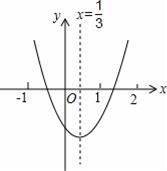
小明从图示的二次函数y=ax2+bx+c的图象中,观察得出了下面4条信息:
①abc>0;②a﹣b+c>0;③2a﹣3b=0;④c﹣4b>0.你认为其中正确信息是 (填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com