
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为 .
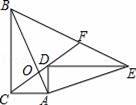

14 .
【考点】旋转的性质.
【分析】根据旋转的性质可得AC=AD,AB=AE,∠CAD=∠BAE,再根据等腰三角形两底角相等求出∠ACD=∠ABE,从而得到△AOC∽△FOB,根据相似三角形对应边成比例求出BF=OB,过点C作CH⊥AB于H,根据等腰三角形三线合一的性质可得AO=2AH,再由△ACH∽△ABC求出AH,然后根据BO=AB﹣AO即可得解.
【解答】解:∵△ABC以点A为旋转中心顺时针旋转得到△ADE,
∴AC=AD,AB=AE,∠CAD=∠BAE(为旋转角),
∵∠ACD=
 (180°﹣∠CAD),∠ABE=
(180°﹣∠CAD),∠ABE=
 (180°﹣∠BAE),
(180°﹣∠BAE),
∴∠ACD=∠ABE,
又∵∠AOC=∠BOF,
∴△AOC∽△FOB,
∴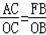
 ,
,
∵AC=OC,
∴BF=OB,
过点C作CH⊥AB于H,则AO=2AH,
∵△ACH∽△ABC,
∴AC2=AH•AB,
∴62=18•AH,
∴AH=2,
∴AO=4,
∴BF=BO=AB﹣AO=18﹣4=14.

【点评】本题考查了旋转的性质,等腰三角形两底角相等的性质,等腰三角形三线合一的性质,利用三角形相似求出BF=OB是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:
将抛物线y=2(x﹣1)2+1向右平移1个单位长度,再向下移1个单位长度,所得的抛物线解析式为( )
A.y=2x2+1 B.y=2(x﹣2)2+2 C.y=2(x﹣2)2 D.y=2x2
查看答案和解析>>
科目:初中数学 来源: 题型:
美丽的雪花扮靓了我们可爱的家乡,但高速公路清雪刻不容缓.某高速公路维护站引进甲、乙两种型号的清雪车,已知甲型清雪车比乙型清雪车每天多清理路段6千米,甲型清雪车清理90千米与乙型清雪车清理60千米路段所用的时间相同.
(1)甲型、乙型清雪车每天各清理路段多少千米?
(2)此公路维护站欲购置甲、乙两种型号清雪车共20台,甲型每台30万元,乙型每台15万元,若在购款不超过360万元,甲型、乙型都购买的情况下,甲型清雪车最多可购买几台?
查看答案和解析>>
科目:初中数学 来源: 题型:
正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图,则图中阴影部分的面积之和等于( )
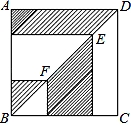
A.a2 B.0.25a2 C.0.5a2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
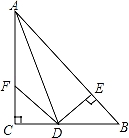
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.说明:
(1)CD=EB;
(2)AB=AF+2EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com