
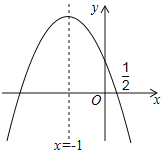
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a+4c=10b;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有错误的结论有( )个.
A.1B.2C.3D.4
【答案】B
【解析】
根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,及运用一些特殊点解答问题.
解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=﹣1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
a﹣2b+4c=a﹣4a+4c=﹣3a+4c,
∵a<0,
∴﹣3a>0,
∴﹣3a+4c>0,
即a﹣2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(﹣![]() ,0),
,0),
当x=﹣![]() 时,y=0,即a(﹣
时,y=0,即a(﹣![]() )2+b×(﹣
)2+b×(﹣![]() )+c=0,
)+c=0,
整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,
∴a﹣b+c>m2a﹣mb+c(m≠﹣1),
∴a﹣b>m(am﹣b),所以⑤正确;
故选:B.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
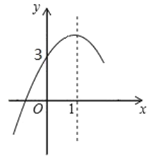
【题目】如图,是二次函数![]() 图象的一部分,对称轴是直线
图象的一部分,对称轴是直线![]() ,与
,与![]() 轴的交点是(0,3),则下列结论中正确的是( )
轴的交点是(0,3),则下列结论中正确的是( )
A.![]() ;B.
;B.![]() >0;C.当0<
>0;C.当0<![]() <2时,
<2时,![]() >3;D.关于
>3;D.关于![]() 的方程
的方程![]() 有两个相等的实数根
有两个相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿楼而过的轻轨、《千与千寻》现实版洪崖洞、空中巴士长江索道……,“3D魔幻城”吸引着海量游客前来重庆打卡.2018年的清明节和“五一”节,洪崖洞入围全球旅游热门目的地榜单,排名仅次于故宫.位于洪崖洞的重庆知名火锅小天鹅火锅在节日期间每天也人满为患,其中鸳鸯火锅和红汤火锅最受游客青睐.在清明节期间,前来就餐选择鸳鸯火锅和红汤火锅的游客共有2200名,鸳鸯火锅和红汤火锅的人均消费分别为130元和120元.
(1)清明节期间,若选择红汤火锅的人数不超过鸳鸯火锅人数的1.5倍.求至少有多少人选择鸳鸯火锅?
(2)“五一”节期间,因天气渐热的原因,前来就餐的游客人数有所下降,与(1)问中选择鸳鸯火锅的人数最少时相比,选择两种火锅的人数均下降了a%;人均消费与清明节期间相比均有所上升,其中鸳鸯火锅的人均消费上涨了a%,红汤火锅的人均消费上涨了![]() %,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
%,最终“五一”节期间两种火锅的总销售额与(1)问中选择鸳鸯火锅的人数最少时的两种火锅的总销售额持平,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
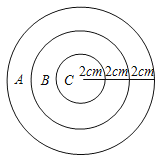
【题目】如图为一个封闭的圆形装置,整个装置内部为A、B、C三个区域(A、B两区域为圆环,C区域为小圆),具体数据如图.
(1)求出A、B、C三个区域三个区域的面积:SA= ,SB= ,SC= ;
(2)随机往装置内扔一粒豆子,多次重复试验,豆子落在B区域的概率PB为多少?
(3)随机往装置内扔180粒豆子,请问大约有多少粒豆子落在A区域?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y=![]() (k≠0)的图象经过点B.
(k≠0)的图象经过点B.
(1)求反比例函数的解析式;
(2)若点E恰好落在反比例函数y=![]() 上,求平行四边形OBDC的面积.
上,求平行四边形OBDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
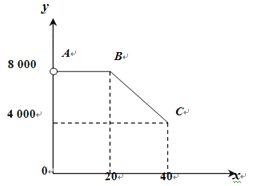
【题目】小张到老王的果园里一次性采购一种水果,他俩商定:小张的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图象如图中的折线段
(吨)之间函数关系的图象如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)已知老王种植水果的成本是![]() 元/吨,那么小张的采购量为多少时,老王在这次买卖中所获的利润
元/吨,那么小张的采购量为多少时,老王在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
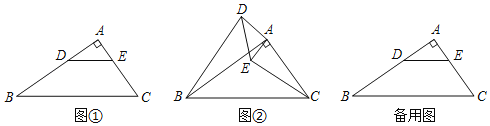
如图①,在Rt△ABC中,∠A=90°,AB=kAC,点D是AB上一点,DE∥BC.
填空:BD,CE的数量关系为 ;位置关系为 ;
(2)类比探究
如图②,将△ADE绕着点A顺时针旋转,旋转角为α(0°<α≤90°),连接BD,CE,请问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
(3)拓展延伸
在(2)的条件下,将△ADE绕点A顺时针旋转,旋转角为α,直线BD,CE交于点F,若AC=1,AB=![]() ,当∠ACE=15°时,请直接写出BF的长.
,当∠ACE=15°时,请直接写出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于A.B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
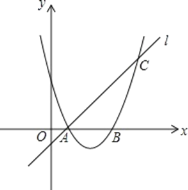
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com