
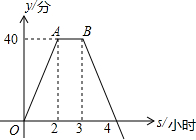
 为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示
为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示分析 (1)根据图象求出表示玩游戏2小时到3小时之间游戏的积分不变;
(2)①当0<x≤2时,设y=kx,求得y=20x,②当2<x≤3时,y=40,③当x>3时,设y=mx+n,根据直线过(3,40),(4,0),求得y=-40x+160,
(3)当y=20时,列方程-20=-40x+160,即可求得结论.
解答 解:(1)线段AB的实际意义是:表示玩游戏2小时到3小时之间游戏的积分不变;
(2)①当0<x≤2时,设y=kx,
∵直线OA过(2,40),
∴y=20x,
②当2<x≤3时,y=40,
③当x>3时,
设y=mx+n,
∵直线过(3,40),(4,0),
∴$\left\{\begin{array}{l}{40=3m+n}\\{0=4m+n}\end{array}\right.$,
∴y=-40x+160,
综上所述:y与x的函数关系式为:y=$\left\{\begin{array}{l}{20x(0<x≤2)}\\{40(2<x≤3)}\\{-40x+160(x>3)}\end{array}\right.$;
(3)当y=20时,-20=-40x+160,
解得:x=4.5,
∴连续上网4.5小时后他的积分数值变为0.
点评 本题考查了待定系数法求一次函数关系式,根据图象得出点的坐标进而求出解析式是解题关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.
如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com