
分析 (1)首先设工厂每月生产x件产品,由题意可得方案一的等量关系是:利润=产品的销售价-成本价-处理废渣的费用-设备的维护和损耗的费用,方案二的等量关系是:利润=产品的销售价-成本价-处理废渣的费用.
(2)当所获得的利润一样时,可得方程x-0.55x-0.05x-20=x-0.55x-0.1x,再解即可;
(3)可将(1)中得出的关系式进行比较,判断出不同的自变量的取值范围内哪个方案最省钱.
解答 解:(1)因为工厂每月生产x件产品,每月利润为y万元,由题意得:
选择方案一时,月利润为y1=x-0.55x-0.05x-20=0.4x-20(x≥50),
选择方案二时,月利润为y2=x-0.55x-0.1x=0.35x(x≥0);
(2)由题意得:
x-0.55x-0.05x-20=x-0.55x-0.1x,
解得:x=400.
答:当工厂每月生产400件产品时,两种方案所获得的利润一样.
(3)若y1>y2,即0.4x-20>0.35x,
解得x>400,
则当月生产量大于400件时,选择方案一所获得利润较大;
则当月生产量等于400件时,两种方案所获得利润一样大;
则当月生产量小于400件时,选择方案二所获得利润较大;
若每月生产600件产品,则方案一使每月利润更大.
故答案为:一.
点评 本题考查了一次函数的应用,解题关键是要列出方案一与方案二的函数关系式.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
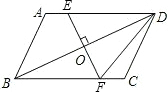 已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.
已知:如图,BD为平行四边形ABCD的对角线,O为BD的中点,EF⊥BD于点O与AD,BC分别交于点E,F.若DE=15cm,CD=13cm,求DF的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
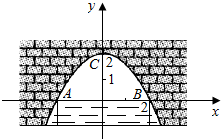 图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
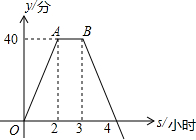 为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示
为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 个人月收入(元) | 1600 | 2400 | 3200 | 4000 | 4800 | … |
| 每月销售量(万件) | 1 | 2 | 3 | 4 | 5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com