
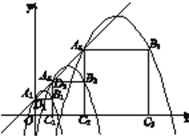
【题目】在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
(1)直接写出下列点的坐标:B1________,B2________,B3________;
(2)写出抛物线L2、L3的解析式,并写出其中一个解析式求解过程,再猜想抛物线Ln的顶点坐标
(3)设A1D1=k1·D1B1,A2D2=k2·D2B2,试判断k1与k2的数量关系并说明理由.
【答案】(1)B1(1,1),B2(3,2),B3(7,4).(2)(![]() ,
, ![]() );(3)k1=k2
);(3)k1=k2
【解析】试题解析:(1)由直线解析式可求得A1的坐标,由正方形的性质则可求得B1坐标,由题意可求得A2的横坐标,则可求得其纵坐标,再利用正方形的性质可求得B2的坐标,同理可求得B3的坐标;
(2)由对称性可求得抛物线的对称轴,则可求得其顶点坐标,再结合已知点的坐标可求得抛物线解析式,可写出L2、L3的解析式;利用An、Bn的变化规律,可求得抛物线Ln的顶点坐标;
(3)由抛物线L2的解析式可求得A1D1的长,则可求得k1,同理可求得k2,从而可求得两者之间的数量关系.
试题解析:解:
(1)∵A1在直线y=x+1上,∴A1的坐标为(0,1),∴A1B1=OA1=1,∴B1(1,1),∴A2横坐标为1,且在直线y=x+1上,∴A2(1,2),∴A2B2=A2C1=2,∴B2(3,2),同理B3(7,4),故答案为:(1,1);(3,2);(7,4);
(2)抛物线L2、L3的解析式分别为y=﹣(x﹣2)2+3,y=﹣![]() (x﹣5)2+6;
(x﹣5)2+6;
抛物线L2的解析式的求解过程如下:
对于直线y=x+1,设x=0,可得y=1,∴A1(0,1),∵四边形A1B1C1O是正方形,∴C1(1,0),又点A2在直线y=x+1上,∴可得点A2(1,2),又∵B2的坐标为(3,2),∴抛物线L2的对称轴为直线x=2,∴抛物线L2的顶点为(2,3),设抛物线L2的解析式为:y=a(x﹣2)2+3,∵L2过点B2(3,2),∴2=a×(3﹣2)2+3,解得a=﹣1,∴抛物线L2的解析式为y=﹣(x﹣2)2+3;
猜想抛物线Ln的顶点坐标为(3×2n﹣2﹣1,3×2n﹣2).
证明如下:
由正方形AnBnCnCn﹣1顶点An,Bn的坐标规律为An(2n﹣1﹣1,2n﹣1)与Bn(2n﹣1,2n﹣1),∴抛物线Ln的对称轴为直线x=![]() =3×2n﹣2﹣1,又顶点在直线y=x+1上,∴y=3×2n﹣2,∴抛物线Ln的顶点坐标为(3×2n﹣2﹣1,3×2n﹣2);
=3×2n﹣2﹣1,又顶点在直线y=x+1上,∴y=3×2n﹣2,∴抛物线Ln的顶点坐标为(3×2n﹣2﹣1,3×2n﹣2);
(3)k1与k2的数量关系为k1=k2.
理由如下:
由(2)得L2的解析式为y=﹣(x﹣2)2+3,当y=1时,1=﹣(x﹣2)2+3,解得x1=![]() ,x2=
,x2=![]() ,∵0<A1D1<1,∴x=
,∵0<A1D1<1,∴x=![]() ,∴A1D1=
,∴A1D1=![]() =
=![]() ,∴D1B1=1﹣(
,∴D1B1=1﹣(![]() )=
)=![]() ,∴A1D1=
,∴A1D1=![]() D1B1,即k1=
D1B1,即k1=![]() ;
;
同理可求得A2D2=![]() =
=![]() ,D2B2=2﹣(4﹣2
,D2B2=2﹣(4﹣2 ![]() )=2
)=2 ![]() ﹣2=2(
﹣2=2(![]() ),∴A2D2=
),∴A2D2=![]() D2B2,即k2=
D2B2,即k2=![]() ,∴k1=k2.
,∴k1=k2.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
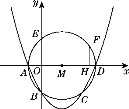
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧ED上的点F作FH⊥AD于点H,且FH=1.5.
(1)求点D的坐标及该抛物线对应的函数表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
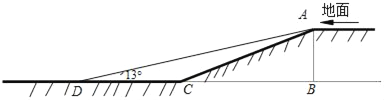
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线C1:y=﹣x2﹣2x,绕着点M(1,0)旋转180°后,所得到的新抛物线C2的解析式是 .
A. y=(x﹣3)2﹣1 B. y=(x﹣3)2+1 C. y=(x+3)2﹣1 D. y=(x﹣3)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
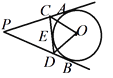
【题目】如图,PA、PB、CD是⊙O的切线,切点分别是A、B、E,CD分别交PA、PB于C、D两点,若∠APB=60°,则∠COD的度数( )
A. 50° B. 60° C. 70° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
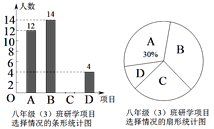
(1)八年级(3)班学生总人数是多少,并将条形统计图补充完整;
(2)宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;
(3)若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
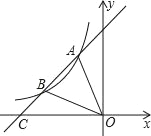
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com