
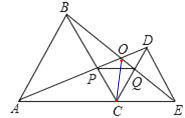
【题目】如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC.以下五个结论:①△ACD≌△BCE;②△AOC≌△BQC ; ③△APC≌△BOC; ④△DPC≌△EQC;⑤ ∠AOB=60°.
其中正确的是( )
A. ①②③④⑤ B. ①④⑤ C. ①④D. ①③④
【答案】B
【解析】
根据角的和差求出∠ACD=∠BCE,结合等边三角形的性质利用SAS可证明△ACD≌△BCE,①正确;求出∠BCQ=60°,可得∠ACO≠∠BCQ,故②错误;同理可得∠ACP≠∠BCO,故③错误;首先证明△CQB≌△CPA,得到CP=CQ,即可证明△DPC≌△EQC,④正确;根据∠CBE=∠DAC利用三角形外角的性质可求出∠AOB=60°,⑤正确.
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD和△BCE中,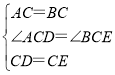 ,
,
∴△ACD≌△BCE(SAS),①正确;
∵∠BCQ=180°-60°-60°=60°,∠ACO=60°+∠BCO,
∴∠ACO≠∠BCQ,
∴△AOC≌△BQC错误,②错误;
∵∠ACP=60°,∠BCO=60°-∠OCQ,
∴∠ACP≠∠BCO,
∴△APC≌△BOC错误,③错误;
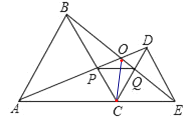
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACP=∠BCQ=60°,AC=BC,
∴△CQB≌△CPA,
∴CP=CQ,
又∵∠PCD=∠QCE=60°,CD=CE,
∴△DPC≌△EQC,④正确;
∵∠CBE=∠DAC,∠CBE+∠AEB=180°-120°=60°,
∴∠AOB=∠DAC+∠AEB=∠CBE+∠AEB=60°,⑤正确,
故选:B.


科目:初中数学 来源: 题型:
【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
(1)在这个问题中,自变量是_ 因变量是_ ;
(2)该轿车油箱的容量为__ L,行驶![]() 时,估计油箱中的剩余油量为____
时,估计油箱中的剩余油量为____![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请估计
,请估计![]() 两地之间的距离.
两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把这个图形称为“8字型”根据三角形内角和容易得到:∠A+∠D=∠C+∠B.


(1)用“8字型”
如图2,∠A+∠B+∠C+∠D+∠E+∠F=___________;
(2)造“8字型”
如图3,∠A+∠B+∠C+∠D+∠E+∠F+∠G=_____________;
(3)发现“8字型”
如图4,BE、CD相交于点A,CF为∠BCD的平分
线,EF为∠BED的平分线.
①图中共有________个“8字型”;
②若∠B:∠D:∠F=4:6:x,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,给出以下六个条件中,以其中三个作为已知条件,不能判断△ABC和△DEF全等的是( ) ①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F;
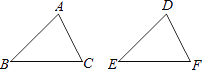
A.①⑤②B.①②③C.④⑥①D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
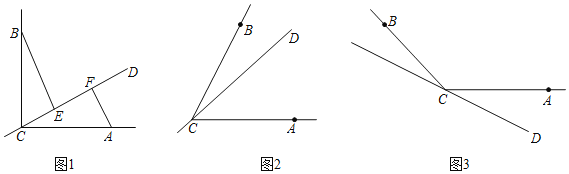
【题目】已知CA=CB,CD是经过∠BCA顶点C的一条直线.E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD在∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,α=90°,则BE CF;EF |BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA数量关系的条件 ,使①中的两个结论仍然成立,补全图形并证明.
(2)如图3,若直线CD在∠BCA的外部,∠BCA=α,请用等式直接写出EF,BE,AF三条线段的数量关系 .(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.
(1)设矩形的相邻两边长分别为x,y.
①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由一些棱长为单位![]() 的相同的小正方体组合成的简单几何体.
的相同的小正方体组合成的简单几何体.
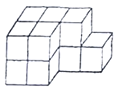
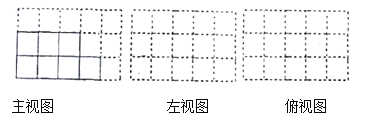
(1)图中有_________块小正方体;
(2)请在相应方格纸中分别画出几何体的左视图和俯视图并用阴影表示出来;
(3)如果在其表面涂漆(几何体放在地上,底面无法涂上漆),则要涂_________平方单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com