
ΓΨΧβΡΩΓΩ“―÷ΣCAΘΫCBΘ§CD «Ψ≠ΙΐΓœBCAΕΞΒψCΒΡ“ΜΧθ÷±œΏΘ°EΘ§F «÷±œΏCD…œΒΡΝΫΒψΘ§«“ΓœBECΘΫΓœCFAΘΫΠΝΘ°
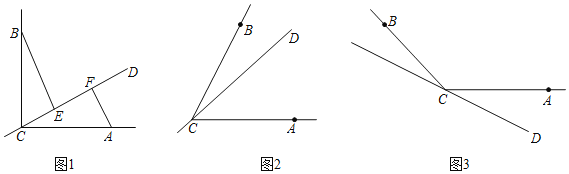
Θ®1Θ©»τ÷±œΏCD‘ΎΓœBCAΒΡΡΎ≤ΩΘ§«“EΘ§F‘Ύ…δœΏCD…œΘ§«κΫβΨωœ¬ΟφΝΫΗωΈ ΧβΘΚ
ΔΌ»γΆΦ1Θ§»τΓœBCAΘΫ90ΓψΘ§ΠΝΘΫ90ΓψΘ§‘ρBEΓΓ ΓΓCFΘΜEFΓΓ ΓΓ|BE©¹AF|Θ®ΧνΓΑΘΨΓ±Θ§ΓΑΘΦΓ±ΜρΓΑΘΫΓ±Θ©ΘΜ
ΔΎ»γΆΦ2Θ§»τ0ΓψΘΦΓœBCAΘΦ180ΓψΘ§«κΧμΦ”“ΜΗωΙΊ”ΎΠΝ”κΓœBCA ΐΝΩΙΊœΒΒΡΧθΦΰΓΓ ΓΓΘ§ ΙΔΌ÷–ΒΡΝΫΗωΫα¬έ»‘»Μ≥…ΝΔΘ§≤Ι»ΪΆΦ–Έ≤Δ÷ΛΟςΘ°
Θ®2Θ©»γΆΦ3Θ§»τ÷±œΏCD‘ΎΓœBCAΒΡΆβ≤ΩΘ§ΓœBCAΘΫΠΝΘ§«κ”ΟΒ» Ϋ÷±Ϋ”–¥≥ωEFΘ§BEΘ§AF»ΐΧθœΏΕΈΒΡ ΐΝΩΙΊœΒΓΓ ΓΓΘ°Θ®≤Μ“Σ«σ÷ΛΟςΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ=Θ§=ΘΜΔΎΠΝ+ΓœBCAΘΫ180ΓψΘ§≤Ι»ΪΆΦ–ΈΚΆ÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©EFΘΫBE+AF
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌ«σ≥ωΓœBECΘΫΓœAFCΘΫ90ΓψΘ§ΓœCBEΘΫΓœACFΘ§ΗυΨίAAS÷ΛΓςBCEΓ’ΓςCAFΘ§ΆΤ≥ωBEΘΫCFΘ§CEΘΫAFΦ¥Ω…ΘΜ
ΔΎ«σ≥ωΓœBECΘΫΓœAFCΘ§ΓœCBEΘΫΓœACFΘ§ΗυΨίAAS÷ΛΓςBCEΓ’ΓςCAFΘ§ΆΤ≥ωBEΘΫCFΘ§CEΘΫAFΦ¥Ω…ΘΜ
Θ®2Θ©«σ≥ωΓœBECΘΫΓœAFCΘ§ΓœCBEΘΫΓœACFΘ§ΗυΨίAAS÷ΛΓςBCEΓ’ΓςCAFΘ§ΆΤ≥ωBEΘΫCFΘ§CEΘΫAFΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΔΌΓΏΓœBCAΘΫ90ΓψΘ§ΓœΠΝΘΫ90ΓψΘ§
ΓύΓœBCE+ΓœCBEΘΫ90ΓψΘ§ΓœBCE+ΓœACFΘΫ90ΓψΘ§
ΓύΓœCBEΘΫΓœACFΘ§
ΓΏCAΘΫCBΘ§ΓœBECΘΫΓœCFAΘ§
ΓύΓςBCEΓ’ΓςCAFΘ®ASAΘ©Θ§
ΓύBEΘΫCFΘ§EFΘΫ|CF©¹CE|ΘΫ||BE©¹AFΘΜ
Ι ¥πΑΗΈΣΘΚΘΫΓΔΘΫΘΜ
ΔΎΠΝ+ΓœBCAΘΫ180ΓψΘ§≤Ι»ΪΆΦ–Έ»γœ¬ΘΚ
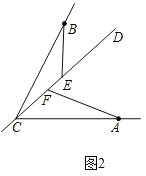
‘ΎΓςBCE÷–Θ§ΓœCBE+ΓœBCEΘΫ180Γψ©¹ΓœBECΘΫ180Γψ©¹ΠΝΘ§
ΓΏΓœBCAΘΫ180Γψ©¹ΠΝΘ§
ΓύΓœBCAΘΫΓœCBE+ΓœBCEΘ§
”÷ΓΏΓœACF+ΓœBCEΘΫΓœBCAΘ§
ΓύΓœCBEΘΫΓœACFΘ§
”÷ΓΏBCΘΫCAΘ§ΓœBECΘΫΓœCFAΘ§
ΓύΓςBCEΓ’ΓςCAFΘ®AASΘ©Θ§
ΓύBEΘΫCFΘ§CEΘΫAFΘ§
”÷ΓΏEFΘΫCE©¹CFΘ§
ΓύEFΘΫ|BE©¹AF|ΘΜ
Ι ¥πΑΗΈΣΘΚΠΝ+ΓœBCAΘΫ180ΓψΘ°
Θ®2Θ©EFΘΫBE+AFΘ§
»γΆΦ3Θ§
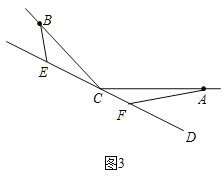
ΓΏΓœBECΘΫΓœCFAΘΫΠΝΘ§ΠΝΘΫΓœBCAΘ§ΓœBCA+ΓœBCE+ΓœACFΘΫ180ΓψΘ§ΓœCFA+ΓœCAF+ΓœACFΘΫ180ΓψΘ§
ΓύΓœBCEΘΫΓœCAFΘ°
”÷ΓΏBCΘΫCAΘ§
ΓύΓςBCEΓ’ΓςCAFΘ®AASΘ©Θ§
ΓύBEΘΫCFΘ§ECΘΫFAΘ§
ΓύEFΘΫEC+CFΘΫBE+AFΘ°
Ι ¥πΑΗΈΣΘΚEFΘΫBE+AFΘ°


 ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
ΩΎΥψΡή ÷œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘΚ![]() ΓΔ
ΓΔ![]() «»ώΫ«
«»ώΫ«![]() ΒΡΝΫΧθΗΏΘ§
ΒΡΝΫΧθΗΏΘ§![]() ΓΔ
ΓΔ![]() Ζ÷±π «
Ζ÷±π «![]() ΓΔ
ΓΔ![]() ΒΡ÷–ΒψΘ§»τEF=6Θ§
ΒΡ÷–ΒψΘ§»τEF=6Θ§![]() .
.
Θ®1Θ©÷ΛΟςΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©≈–Εœ![]() ”κ
”κ![]() ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘΜ
ΒΡΈΜ÷ΟΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘΜ
Θ®3Θ©«σ![]() ΒΡ≥Λ.
ΒΡ≥Λ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΘ§
÷αΘ§![]() ÷αΒΡΫΜΒψΖ÷±πΈΣ
÷αΒΡΫΜΒψΖ÷±πΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΝΫΧθ÷±œΏΒΡΫΜΒψΈΣ
Θ§ΝΫΧθ÷±œΏΒΡΫΜΒψΈΣ![]() Θ§Βψ
Θ§Βψ![]() «œΏΕΈ
«œΏΕΈ![]() …œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ
…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§ΫΜ
÷αΘ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() .
.
![]() «σ
«σ![]() ΒΡΟφΜΐΘΜ
ΒΡΟφΜΐΘΜ
![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψ
…œ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΥΡ±Ώ–Έ
Θ§ ΙΥΡ±Ώ–Έ![]() ΈΣΨΊ–ΈΘ§»τ¥φ‘ΎΘ§«σ≥ω
ΈΣΨΊ–ΈΘ§»τ¥φ‘ΎΘ§«σ≥ω![]() ΒψΉχ±ξΘΚ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
ΒψΉχ±ξΘΚ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
![]() »τΥΡ±Ώ–Έ
»τΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§…η
Θ§…η![]() ΒψΒΡΉχ±ξΈΣ
ΒψΒΡΉχ±ξΈΣ![]() Θ§«σ≥ω
Θ§«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩ
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
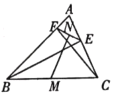
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§CΈΣœΏΕΈAE…œ“ΜΕ·ΒψΘ®≤Μ”κΒψAΘ§E÷ΊΚœΘ©Θ§‘ΎAEΆ§≤ύΖ÷±πΉςΒ»±ΏΓςABCΚΆΒ»±ΏΓςCDEΘ§AD”κBEΫΜ”ΎΒψOΘ§AD”κBCΫΜ”ΎΒψPΘ§BE”κCDΫΜ”ΎΒψQΘ§Ν§Ϋ”PQΘ§OCΘ°“‘œ¬ΈεΗωΫα¬έΘΚΔΌΓςACDΓ’ΓςBCEΘΜΔΎΓςAOCΓ’ΓςBQC ; ΔέΓςAPCΓ’ΓςBOC; ΔήΓςDPCΓ’ΓςEQC;Δί ΓœAOBΘΫ60ΓψΘ°
Τδ÷–’ΐ»ΖΒΡ «Θ® Θ©
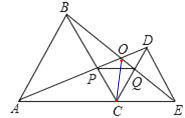
A. ΔΌΔΎΔέΔήΔί B. ΔΌΔήΔί C. ΔΌΔήD. ΔΌΔέΔή
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
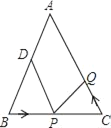
ΓΨΧβΡΩΓΩ»γΆΦΓςABCΘ§ABΘΫACΘΫ24άεΟΉΘ§ΓœBΘΫΓœCΘ§BCΘΫ16άεΟΉΘ§ΒψDΈΣABΒΡ÷–ΒψΘ°ΒψP‘ΎœΏΕΈBC…œ“‘4άεΟΉ/ΟκΒΡΥΌΕ»”…BΒψœρCΒψ‘ΥΕ·Θ§Ά§ ±Θ§ΒψQ‘ΎœΏΕΈCA…œ”…CΒψœρAΒψ‘ΥΕ·Θ°»τΒψQΒΡ‘ΥΕ·ΥΌΕ»ΈΣvάεΟΉ/ΟκΘ§‘ρΒ±ΓςBPD”κΓςCQP»ΪΒ» ±Θ§vΒΡ÷ΒΈΣ_____ άεΟΉ/ΟκΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§―ß–Θ”–“ΜΩι≥ΛΖΫ–ΈΩ’ΒΊΘ§ΥϋΒΡ≥ΛΚΆΩμΒΡ±» «3ΘΚ1Θ§ΟφΜΐΈΣ363![]() .
.
Θ®1Θ©«σΗΟ≥ΛΖΫ–ΈΒΡ≥ΛΚΆΩμΘΜ
Θ®2Θ©»γΆΦΥυ ΨΘ§ΙΛ»Υ ΠΗΒ“Σ‘Ύ’βΩιΩ’ΒΊ…œ…ηΦΤ“ΜΗω‘≤–Έ«χ”ρΚΆΥΡΗω…»–Έ«χ”ρΫχ––¬ΧΜ·Θ§Τδ÷–ΥΡΗω…»–Έ«χ”ρΒΡΑκΨΕ”κ÷–Φδ‘≤–Έ«χ”ρΑκΨΕœύΆ§Θ§»τ¬ΧΜ·«χ”ρΒΡΉήΟφΜΐΈΣ![]() Θ§«κΡψΑο÷ζΙΛ»Υ ΠΗΒΦΤΥψ“Μœ¬÷–Φδ‘≤–Έ«χ”ρΒΡ÷±ΨΕ.
Θ§«κΡψΑο÷ζΙΛ»Υ ΠΗΒΦΤΥψ“Μœ¬÷–Φδ‘≤–Έ«χ”ρΒΡ÷±ΨΕ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœCΘΫ90ΓψΘ§ΓœBΘΫ30ΓψΘ§“‘ΒψAΈΣ‘≤–ΡΘ§»Έ“β≥ΛΈΣΑκΨΕΜ≠ΜΓΖ÷±πΫΜABΘ§AC”ΎΒψMΚΆNΘ§‘ΌΖ÷±π“‘ΒψMΘ§NΈΣ‘≤–ΡΘ§¥σ”Ύ![]() MNΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΝΫΜΓΫΜ”ΎΒψPΘ§Ν§Ϋ”AP≤Δ―”≥ΛΫΜBC”ΎΒψDΘ§‘ρœ¬Ν–ΥΒΖ®ΘΚΔΌAD «ΓœBACΒΡΤΫΖ÷œΏΘΜΔΎΓœADCΘΫ60ΓψΘΜΔέΒψD‘ΎABΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘΜΔήSΓςDACΘΚSΓςABCΘΫ1ΘΚ3.Τδ÷–’ΐ»ΖΒΡ «__________________Θ°(ΧνΥυ”–’ΐ»ΖΥΒΖ®ΒΡ–ρΚ≈)
MNΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΝΫΜΓΫΜ”ΎΒψPΘ§Ν§Ϋ”AP≤Δ―”≥ΛΫΜBC”ΎΒψDΘ§‘ρœ¬Ν–ΥΒΖ®ΘΚΔΌAD «ΓœBACΒΡΤΫΖ÷œΏΘΜΔΎΓœADCΘΫ60ΓψΘΜΔέΒψD‘ΎABΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘΜΔήSΓςDACΘΚSΓςABCΘΫ1ΘΚ3.Τδ÷–’ΐ»ΖΒΡ «__________________Θ°(ΧνΥυ”–’ΐ»ΖΥΒΖ®ΒΡ–ρΚ≈)

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
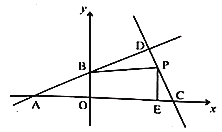
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“Μ¥ΈΚ· ΐy=©¹ax+bΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσœύΫΜ”ΎΒψAΘ®©¹4Θ§©¹2Θ©Θ§BΘ®mΘ§4Θ©Θ§”κy÷αœύΫΜ”ΎΒψCΘ°
ΒΡΆΦœσœύΫΜ”ΎΒψAΘ®©¹4Θ§©¹2Θ©Θ§BΘ®mΘ§4Θ©Θ§”κy÷αœύΫΜ”ΎΒψCΘ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©«σΒψCΒΡΉχ±ξΦΑΓςAOBΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AΘ®-4Θ§![]() Θ©,BΘ®-1Θ§2Θ© «“Μ¥ΈΚ· ΐy=kx+bΒΡΆΦœώ”κΖ¥±»άΐΚ· ΐ
Θ©,BΘ®-1Θ§2Θ© «“Μ¥ΈΚ· ΐy=kx+bΒΡΆΦœώ”κΖ¥±»άΐΚ· ΐ![]() Θ®mΓΌ0Θ§mΘΦ0Θ©ΒΡΚ· ΐΆΦœώΒΡΝΫΗωΫΜΒψΘ§ACΓΆx÷α”ΎΒψCΘ§BDΓΆy÷α”ΎΒψD
Θ®mΓΌ0Θ§mΘΦ0Θ©ΒΡΚ· ΐΆΦœώΒΡΝΫΗωΫΜΒψΘ§ACΓΆx÷α”ΎΒψCΘ§BDΓΆy÷α”ΎΒψD
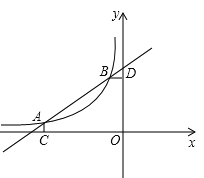
Θ®1Θ©ΗυΨίΚ· ΐΆΦœώ÷±Ϋ”ΜΊ¥πΈ ΧβΘΚ‘ΎΒΎΕΰœσœόΡΎΘ§Β±x»ΓΚΈ÷Β ±Θ§“Μ¥ΈΚ· ΐΒΡ÷Β¥σ”ΎΖ¥±»άΐΚ· ΐΒΡ÷ΒΘΩ
Θ®2Θ©«σ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΦΑmΒΡ÷ΒΘΜ
Θ®3Θ©ΒψP «œΏΕΈAB…œ“ΜΒψΘ§Ν§Ϋ”PC,PD,»τΓςPCAΚΆΓςPBDΒΡΟφΜΐœύΒ»Θ§«σΒψPΒΡΉχ±ξΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com