练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个多边形的一个外角为α，且该多边形的内角和与α的和等于840°，则这个多边形的边数为_____，α=_____度．

    【答案】六； 120．

    【解析】

    多边形外角一定小于180°，利用840除以180可得4余120，可得这个多边形的边数为6，外角α是120°．

    ∵840÷180=4…120，

    ∴这个多边形的边数为：4+2=6，

    α=120°，

    故答案为：六；120．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（　　）
    A.16个
    B.20个
    C.25个
    D.30个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果不等式(a－1)x>a－1的解集是x<1，那么a的取值范围是(　　)

    A. a≤1B. a<1C. a≥1D. a<0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小丽去糖果店买糖果，她买n斤硬糖，每斤a元，买m斤软糖，每斤b元，则她共需付元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.

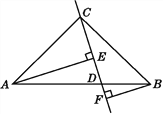
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图一：在Rt△ABC中，∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线，AD、BE交于点F，过F点做FH⊥AD交AC于点H，易证：AH+DB=AB;

    （1）若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线，即：AF、BF分别是∠BAC、∠ABC的外角平分线交于F点，FH⊥AF交直线AC于H点，如图二:请写出线段AH、BD、AB之间的数量关系，并证明。

    （2）若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线，即：AF是∠A的内角平分线，BE是∠B的外角平分线交于F点，FH⊥AD交AC于点H.如图三：请写出线段AH、BD、AB之间的数量关系，无需证明。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，边长为1，∠A=60°，顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…，则四边形A2016B2016C2016D2016的面积是 ．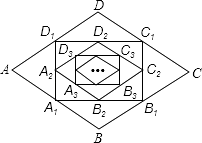

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：2a3+8a2b+8ab2=_____．

    查看答案和解析>>

    同步练习册答案