
 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,求证:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形.
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,求证:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形. 分析 ①由等边三角形的性质得出AB=DB,∠ABD=∠CBE=60°,BE=BC,得出∠ABE=∠DBC,由SAS即可证出△ABE≌△DBC;
②由△ABE≌△DBC,得出∠BAE=∠BDC,根据三角形外角的性质得出∠DMA=60°;
③由ASA证明△ABP≌△DBQ,得出对应边相等BP=BQ,即可得出△BPQ为等边三角形;
解答 证明:①∵△ABD、△BCE为等边三角形,
∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
在△ABE和△DBC中,
$\left\{\begin{array}{l}{AB=DB}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△DBC(SAS),
②∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°-60°-60°=60°,
∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
③在△ABP和△DBQ中,
$\left\{\begin{array}{l}{∠BAP=∠BDQ}\\{AB=DB}\\{∠ABP=∠DBQ=60°}\end{array}\right.$,
∴△ABP≌△DBQ(ASA),
∴BP=BQ,
∴△BPQ为等边三角形.
点评 此题考查了等边三角形的判定与性质与全等三角形的判定与性质,平行线的判定和性质,此题图形比较复杂,解题的关键是仔细识图,找准全等的三角形.


科目:初中数学 来源: 题型:填空题
| 种子粒数 | 100 | 500 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 470 | 948 | 1912 | 2853 |
| 发芽频率 | 0.96 | 0.94 | 0.948 | 0.956 | 0.951 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
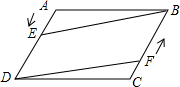 如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.
如图,在?ABCD中,点E从A向D运动,点F从C向B运动,点E的运动速度m与点F的运动速度n满足m=n关系时,四边形BEDF为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
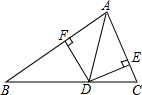 如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.
如图,点D是BC边上的点,DE⊥AB于E,DF⊥AC于F,AE=AF,连接AD,已知△ABD的面积为s1,△ACD的面积为s2,BC=a,AC=b,AB=c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com