
问题情境:如图1,直角三角板ABC中,∠C=90°,AC=BC,将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上,再将该直角绕点D旋转,并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究:(1)在旋转过程中,
①如图2,当AD=BD时,线段DP、DQ有何数量关系?并说明理由。
②如图3,当AD=2BD时,线段DP、DQ有何数量关系?并说明理由。
③根据你对①、②的探究结果,试写出当AD=nBD时,DP、DQ满足的数量关系为_______________(直接写出结论,不必证明)
(2)当AD=BD时,若AB=20,连接PQ,设△DPQ的面积为S,在旋转过程中,S是否存在最小值或最大值?若存在,求出最小值或最大值;若不存在,请说明理由。
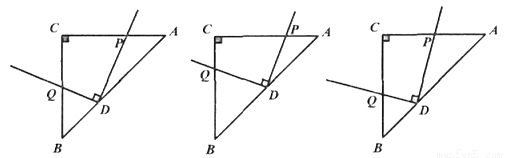
图1 图2 图3
(1)① DP=DQ ②DP=2DQ ③DP=nDQ (2)当DP⊥AC时,x最小,最小值是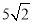 ,此时,S有最小值,
,此时,S有最小值, 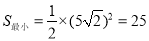 当点P与点A重合时,x最大,最大值是10,此时,S有最大值,
当点P与点A重合时,x最大,最大值是10,此时,S有最大值,
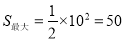
【解析】
试题分析:此题主要考查了等腰直角三角形的性质和相似三角形的判定和性质以及二次函数最值求出等知识,熟练利用相似三角形的性质得出对应边关系是解题关键.
(1)①首先利用等腰直角三角形的性质得出△ADP≌△CDQ(ASA),即可得出答案;
②首先得出△DPM∽△DQN,则  ,求出△AMD∽△BND,进而得出答案.
,求出△AMD∽△BND,进而得出答案.
③根据已知得出Rt△DNP∽Rt△DMQ,则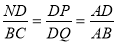 ,则AD=nBD,求出即可;
,则AD=nBD,求出即可;
(2)当DP⊥AC时,x最小,最小值是5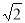 .此时,S有最小值;当点P与点A重合时,x最大,最大值为10,分别求出即可.
.此时,S有最小值;当点P与点A重合时,x最大,最大值为10,分别求出即可.
试题解析:(1)①DP=DQ
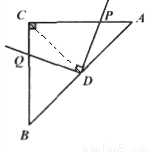
理由:连接CD,
∵AD=BD,△ABC是等腰直角三角形,
∴AD=CD,∠A=∠DCQ,∠ADC=90°,∴∠ADP+∠PDC=∠CDQ+∠PDC=90°,
∴∠ADP=∠CDQ,∴△ADP≌△CDQ,∴DP=DQ.
② DP= 2DQ 。
理由:如图,过点D作DM⊥AC、DN⊥BC,垂足分别为M、N,
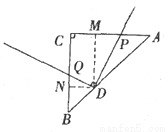
∴∠DMP=∠DNQ=90°,∠MDP=∠NDQ,
∴△DPM∽△DQN,∴DM:DN=DP:DQ 。
∵∠AMD=∠DNB=90°,∠A=∠B,
∴△AMD∽△BND,∴AD:BD=DM:DN。
∴DP:DQ=AD:BD=2BD:BD=2:1,
∴DP=2DQ。
③DP=NQ。
(2)存在,设DQ=x,由(1)①知DP=x,
∴S=1/2xx=1/2x2
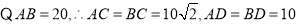 ,
,
当DP⊥AC时,x最小,最小值是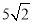 ,此时,S有最小值,
,此时,S有最小值,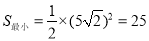
当点P与点A重合时,x最大,最大值是10,此时,S有最大值,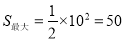
考点:几何变换综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届北京市大兴区八年级下学期期末考试数学试卷(解析版) 题型:解答题
己知一元二次方程x2﹣3x+m﹣1=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程有两个相等的实数根,求此时方程的根.
查看答案和解析>>
科目:初中数学 来源:2015届云南省八年级上学期期末考试数学试卷(解析版) 题型:选择题
下列计算中,运算正确的有几个( )
(1) 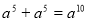
(2) 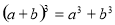
(3) 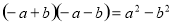 ]
]
(4)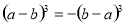
(5)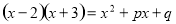 ,则
,则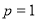 ,
,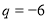
A、4个 B、3个 C、2个 D、1个
查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:解答题
为响应吉安市2014年创建国家级卫生城市的号召,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图。
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率。

查看答案和解析>>
科目:初中数学 来源:2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷(解析版) 题型:填空题
在△ABC中,点I是内心,若∠A=40°,则∠BIC的度数为__________。
查看答案和解析>>
科目:初中数学 来源:2014年北京市西城区中考二模数学试卷(解析版) 题型:解答题
据报道:2013年底我国微信用户规模已到达6亿.以下是根据相关数据制作的统计图表的一部分:
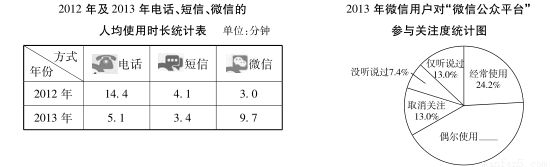
请根据以上信息,回答以下问题:
(1)从2012年到2013年微信的人均使用时长增加了________分钟;
(2)补全2013年微信用户对“微信公众平台”参与关注度扇形统计图,在我国6亿微信用户中,经常使用户约为_________亿(结果精确到0.1);
(3)从调查数学看,预计我国微信用户今后每年将以20%的增长率递增,请你估计两年后,我国微信用户的规模将到达_________亿.
查看答案和解析>>
科目:初中数学 来源:2014年北京市海淀区中考二模数学试卷(解析版) 题型:选择题
如图,AB∥CD,点E在CA的延长线上.若∠BAE=40°,则∠ACD的大小为( )

A.150° B.140° C.130° D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com