
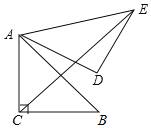
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AB=4,将△ABC绕点A逆时针旋转60°,得到△ADE,连接CE,则CE等于( )
A. 5B. 6C. 2+2![]() D. 2+2
D. 2+2![]()
【答案】C
【解析】
首先考虑到CE所在的三角形并不是特殊三角形,所以猜想到要求CE,可能需要构造直角三角形.由旋转的性质可知,AB=AE,∠BAE=60°,故△ABE是等边三角形,可证明△ACE与△CBE全等,可得到∠ACE=45°,∠AEC=30°,再证△AFC和△AFE是直角三角形,然后在根据勾股定理求解.
连结BE,设CE与AB相交于点F,如下图所示,

∵Rt△ABC中,AC=BC,∠ACB=90°
∴∠CBA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AB=AE
又∵旋转角为60°
∴∠CAD=∠BAE=60°,
∴△ABE是等边三角形
∴AB=BE=AE=4
在△ACE与△CBE中,
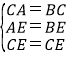
∴△ACE≌△CBE (SSS)
∴∠ACE=∠CBE=45°,∠CEB=∠AEC=30°
∴在△ACF中,∠CFA=180°-45°-45°=90°
∴∠AFC=∠AFE=90°
∴CF⊥AB,∵CA=CB,∠ACB=90°,
∴CF=AF=FB=2,
又在Rt△AFE中,∠AEF=30°,
∴FE=![]() AF=2
AF=2![]() ,
,
∴CE=CF+FE=2+2![]() .
.
故选C.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
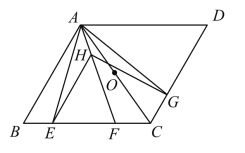
【题目】如图,在菱形ABCD中,AB=AC,点E、F、G分别在边BC、CD上,BE=CG,AF平分∠EAG,点H是线段AF上一动点(与点A不重合).
(1)求证:△AEH≌△AGH;
(2)当AB=12,BE=4时:
①求△DGH周长的最小值;
②若点O是AC的中点,是否存在直线OH将△ACE分成三角形和四边形两部分,其中三角形的面积与四边形的面积比为1:3.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国淡水资源短缺问题十分突出,节约用水已成为各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区10户家庭的月用水量,结果如表所示:
月用水量(t) | 3 | 4 | 5 | 10 |
户数 | 4 | 2 | 3 | 1 |
这10户家庭月用水量的平均数、中位数及众数是( )
A. 4.5,3,4B. 3,4.5,4C. 4.5,4,3D. 4,4.5,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 分别与x轴,y轴交于点
分别与x轴,y轴交于点![]() ,点C是第一象限内的一点,且
,点C是第一象限内的一点,且![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点,与x轴的另一交点为D.
两点,与x轴的另一交点为D.
(1)求此抛物线的解析式;
(2)判断直线![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以![]() 四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿坡角为30°的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈
米处的点C出发,沿坡角为30°的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,计算结果保留根号)
,计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BAC=90°,E是AC的中点,AE=2.经过点E作△ABE外接圆的切线交BC于点D,过点C作CF⊥BC交BE的延长线于点F,连接FD交AC于点H,FD平分∠BFC.
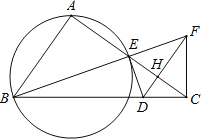
(1)求证:DE=DC;
(2)求证:HE=HC=1;
(3)求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 沿弦
沿弦![]() 折叠,使折叠后的劣弧
折叠,使折叠后的劣弧![]() 恰好经过圆心O,连接
恰好经过圆心O,连接![]() 并延长交
并延长交![]() 于点C,点P是优弧
于点C,点P是优弧![]() 上的动点,连接
上的动点,连接![]() .
.
(1)如图,用尺规面出折叠后的劣弧![]() 所在圆的圆心
所在圆的圆心![]() ,并求出
,并求出![]() 的度数;
的度数;
(2)如图,若![]() 是
是![]() 的切线,
的切线,![]() ,求线段
,求线段![]() 的长;
的长;
(3)如图,连接![]() ,过点B作
,过点B作![]() 的重线,交
的重线,交![]() 的延长线于点D,求证:
的延长线于点D,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点A在x轴的正半轴上,菱形ABCD的边长为2,顶点C的坐标为![]() .
.
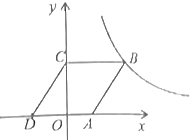
(1)求图像过点B的反比例函数的解析式;
(2)求图像过点A,B的一次函数的解析式;
(3)在第一象限内,当以上所求一次函数的图像在所求反比例函数的图像下方时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com