
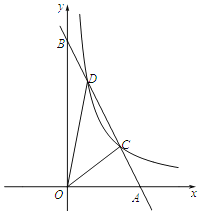
【题目】如图,已知直线y=﹣2x+4与x轴交于点A,与y轴交于点B,与双曲线y=![]() (x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为_____.
(x>0)交于C、D两点,且∠AOC=∠ADO,则k的值为_____.
【答案】![]()
【解析】
先利用面积判断出BD=AC,再判断出△AOC∽△ADO,进而建立方程求出AC=BD,再判断出△ACE∽△ABO,进而求出CE,OE,即可得出结论.
解:由已知得OA=2,OB=4,根据勾股定理得出,AB=2![]() ,
,
如图,过点C作CE⊥x轴于E,作CG⊥y轴G,过点D作DH⊥x轴于H,作DF⊥y轴于F,连接GH,GD,CH,
∵点C,D是反比例图象上的点,
∴S矩形FDHO=S矩形GCEO,
∴![]() S矩形FDHO=
S矩形FDHO=![]() S矩形GDEO.
S矩形GDEO.
∴S△DGH=S△GHC.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BDHG和四边形GHAC都是平行四边形.
∴BD=GH,GH=CA.
即BD=AC;
设AC=BD=m,
∵∠AOC=∠ADO,
CAO=∠DAO,
∴△AOC∽△ADO,
∴![]() ,
,
∴AO2=ACAD,
∴22=m(2![]() ﹣m),
﹣m),
∴m=![]() ±1(舍去
±1(舍去![]() +1),
+1),
过点C作CE⊥x轴于点E,
∴△ACE∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,CE=
,CE=![]() ,
,
∴OE=OA﹣AE=2﹣![]() =
=![]() OE=
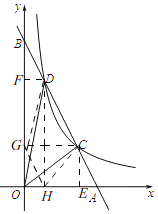
OE=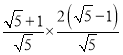 =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
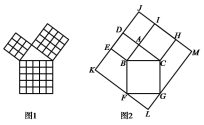
【题目】在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,![]() ,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的![]() ,
,![]() .如果跳蚤开始时在
.如果跳蚤开始时在![]() 边的
边的![]() 处,
处,![]() .跳蚤第一步从
.跳蚤第一步从![]() 跳到
跳到![]() 边的
边的![]() (第1次落点)处,且
(第1次落点)处,且![]() ;第二步从
;第二步从![]() 跳到
跳到![]() 边的
边的![]() (第2次落点)处,且
(第2次落点)处,且![]() ;第三步从
;第三步从![]() 跳到
跳到![]() 边的
边的![]() (第3次落点)处,且
(第3次落点)处,且![]() ;……;跳蚤按上述规则一直跳下去,第
;……;跳蚤按上述规则一直跳下去,第![]() 次落点为
次落点为![]() (
(![]() 为正整数),则点
为正整数),则点![]() 与
与![]() 之间的距离为( )
之间的距离为( )
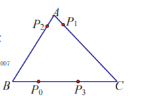
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发市场内有一种水果,保鲜期一周,如果冷藏,可以延长保鲜时间,但每天仍有一定数量的这种水果变质,假设这种水果保鲜期内的个体重量基本保持不变。现有一个体户,按市场价收购了这种水果200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后这种鲜水果每千克的价格每天可上涨0.2元,但存放一天需各种费用20元,日平均每天还有1千克变质丢弃.
(1)设![]() 天后每千克鲜水果的市场价
天后每千克鲜水果的市场价![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若存放![]() 天后将鲜水果一次性出售,设鲜水果的销售总金额为
天后将鲜水果一次性出售,设鲜水果的销售总金额为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)该个体户将这批水果存放多少天后出售,可获最大利润![]() ?最大利润
?最大利润![]() 是多少?
是多少?
(本题不要求写出自变量![]() 的取值范围)
的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
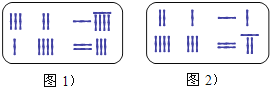
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
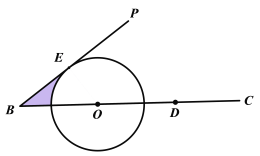
【题目】如图,已知∠PBC,在射线BC上任取一点D,以线段BD的中点O为圆心作⊙O,且⊙O与PB相切于点E.
(1)求作:射线BP上一点A,使△ABD为等腰三角形,且AB=AD.(要求:运用直尺和圆规,保留作图痕迹,不写作法)
(2)求证:AD是⊙O的切线.
(3)若BD的长为8cm,∠PBC=30°,求阴影部分的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )

A.∠A=60°B.△ACD是直角三角形
C.BC=![]() CDD.点B是△ACD的外心
CDD.点B是△ACD的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
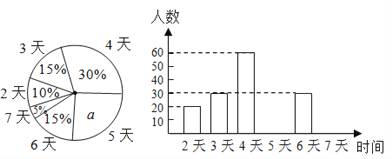
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校初一学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)在这次抽样调查中,众数和中位数分别是多少?
(5)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com