
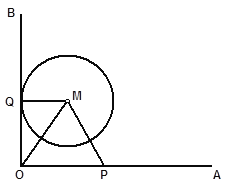
【题目】如图,射线OA⊥射线OB,半径![]() 的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM
的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM![]() .设OP=
.设OP= ![]()
![]() ,OQ=
,OQ= ![]()
![]() .
.
(1)求![]() 、
、![]() 所满足的关系式,并写出
所满足的关系式,并写出![]() 的取值范围 ;
的取值范围 ;
(2)当△MOP为等腰三角形时,求相应![]() 的值;
的值;
(3)是否存在大于2的实数![]() ,使△MQO∽△OMP?若存在,求相应
,使△MQO∽△OMP?若存在,求相应![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() ,使△MQO∽△MOP
,使△MQO∽△MOP
【解析】试题分析:(1)过点M作MD⊥OA,垂足为D,可以知道△MDP为直角三角形,DP=(x-2)cm,MD=ycm,勾股定理即可得出x、y所满足的关系式,并写出x的取值范围;(2)若△MOP为等腰三角形,①若OM=MP,则有OD=PD,此时x=2×2=4;②若MP=OP时,x=3;③若OM=OP时,OM=4+y2,结合(1)求出x的值;(3)△MQO∽△OMP,因为∠Q=90°,∠OMP=90°,根据相似比及(1)的关系式求相应x的值.
试题解析: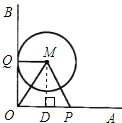
(1)过点M作MD⊥OA,垂足为D,显然ODMQ为矩形,
∴OD=MQ=2,MD=OQ=y,
∴PD=x2,
在Rt△MDP中,y2+(x2)2=32,
∴x24x+y2=5,
当如图所示情况时,OD=2;
当M与OA相切时,
可知OP=2+![]() ,
,
∴x取值范围为0x<2+![]() ;
;
(2)①若OM=MP,此时x=4,
②若MP=OP时,此时x=3,
③若OM=OP时,
∵OM=4+y2,
∴4+y2=x2,
∴![]() ,
,
解得x=![]() ;
;
(3)∵△QMO∽△MOP,此时∠OMP=90°,则![]() ,
,
∴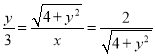 ,
,
∴4+y2=2x,
∴![]() ,
,
∴x=1+![]() <2
<2![]() ,
,
∴存在这样的实数x,并且x=1+![]() .
.


科目:初中数学 来源: 题型:
【题目】一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,设慢车离乙地为y1(km),快车离乙地的距离为y2(km),慢车行驶时间为x(h),两车之间的距离为s(km),y1 ,y2与x的函数关系图像如图①所示,s与x的函数关系图如图②所示:

图① 图②
(1)图中的a= ,b= .
(2)求s关于x的函数关系式.
(3)甲、乙两地间有E、F两个加油站,相距200km,若慢车进入加油站E时,快车恰好进入加油站F,请直接写出加油站E到甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4 , 则S1+S2+S3+S4= . 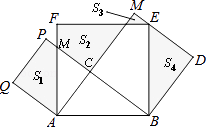
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”,将数据3万亿美元用科学记数法表示为( )
A.3×1014美元
B.3×1013美元
C.3×1012美元
D.3×1011美元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 在同一平面内,过一点有且只有一条直线与已知直线平行
B. 在同一平面内,过一点有且只有一条直线与已知直线垂直
C. 从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D. 不相交的两条线段是平行线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com