
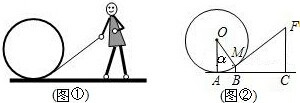
 如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.
如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.| FN |
| FM |

| FN |
| FM |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
 已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论:
已知正方形ABCD中点E,F分别在边AD,DC上,∠EBC=∠BEF,连接BD.下列结论:| 1 |
| 2 |
| 1 |
| 8 |
| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
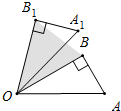 如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为
如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com