
【题目】如图1,在平面直角坐标系中,已知点![]() ,以O为圆心,OA为半径作
,以O为圆心,OA为半径作![]() ,交y轴于点C,直线l:
,交y轴于点C,直线l:![]() 经过点C.
经过点C.
![]() 设直线l与
设直线l与![]() 的另一个交点为
的另一个交点为![]() 如图
如图![]() ,求弦CD的长;
,求弦CD的长;
![]() 将直线l向上平移2个单位,得直线m,如图2,求证:直线m与
将直线l向上平移2个单位,得直线m,如图2,求证:直线m与![]() 相切;
相切;
![]() 在
在![]() 的前提下,设直线m与
的前提下,设直线m与![]() 切于点P,Q为
切于点P,Q为![]() 上一动点,过点P作
上一动点,过点P作![]() ,交直线QA于点
,交直线QA于点![]() 如图
如图![]() ,则
,则![]() 的最大面积为______.
的最大面积为______.

【答案】![]() ;
;![]() 证明见解析;
证明见解析;![]() 54.
54.
【解析】
![]() 过点O作
过点O作![]() ,垂足为E,设直线l与x轴交于点B,利用面积法求出OE,再利用勾股定理求出CE即可解决问题;
,垂足为E,设直线l与x轴交于点B,利用面积法求出OE,再利用勾股定理求出CE即可解决问题;
![]() 过点O作
过点O作![]() ,垂足为F,设直线m与x轴交于点N,与y轴交于点M,
,垂足为F,设直线m与x轴交于点N,与y轴交于点M,![]() 如图
如图![]() ,只要证明
,只要证明![]() 半径即可解决问题;
半径即可解决问题;
![]() 设
设![]() 与x轴的另一交点为G,连接PA、OP、PG,过点P作
与x轴的另一交点为G,连接PA、OP、PG,过点P作![]() 轴于H,
轴于H,![]() 如图
如图![]() ,由
,由![]() ≌
≌![]() ,推出
,推出![]() ,由
,由![]() ,
,![]() ,可得
,可得![]() ,推出当PQ取得最大值时,即
,推出当PQ取得最大值时,即![]() 时,
时,![]() 取得最大值.
取得最大值.
![]() 解:过点O作
解:过点O作![]() ,垂足为E,设直线l与x轴交于点B,
,垂足为E,设直线l与x轴交于点B,![]() 如图
如图![]()
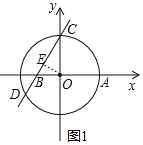
![]() 直线l:
直线l:![]() 经过点
经过点![]() ,
,
![]() ,直线l为
,直线l为![]() ,
,
由![]() 得,
得,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 证明:过点O作
证明:过点O作![]() ,垂足为F,设直线m与x轴交于点N,与y轴交于点M,
,垂足为F,设直线m与x轴交于点N,与y轴交于点M,![]() 如图
如图![]()

![]() 直线m由直线l向上平移2个单位得到,
直线m由直线l向上平移2个单位得到,
![]() 直线m为
直线m为![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线m与
直线m与![]() 相切.
相切.
![]() 的最大面积为54.
的最大面积为54.
理由:设![]() 与x轴的另一交点为G,连接PA、OP、PG,过点P作
与x轴的另一交点为G,连接PA、OP、PG,过点P作![]() 轴于H,
轴于H,![]() 如图
如图![]()
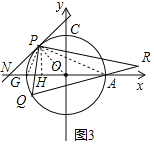
由![]() ∽
∽![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 当PQ取得最大值时,即
当PQ取得最大值时,即![]() 时,
时,![]() 取得最大值,
取得最大值,
此时![]() .
.
故答案为54.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图(1),已知A(a,0),B(0,b),且满足a=![]() .
.
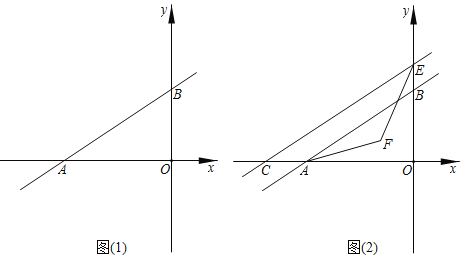
(1)求A、B两点坐标;
(2)在(1)的条件下,Q为直线AB上一点,且满足S△AOQ=2S△BOQ,求Q点的纵坐标;
(3)如图(2),E点在y轴上运动,且在B点上方,过E作AB的平行线,交x轴于点C,∠CEO的平分线与∠BAO的平分线交于点F.问:点E在运动过程中,∠F的大小是否发生改变?若改变,请说明理由;若不变,请求出它的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是等边三角形,
是等边三角形,![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为顶点做
为顶点做![]() .
. ![]() 交过
交过![]() 且平行于
且平行于![]() 的直线于
的直线于![]() ,求证:
,求证:![]() ;当
;当![]() 为
为![]() 的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取
的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取![]() 的中点
的中点![]() ,连结
,连结![]() ,然后证明
,然后证明![]() . 从而得到
. 从而得到![]() ,我们继续来研究:
,我们继续来研究:
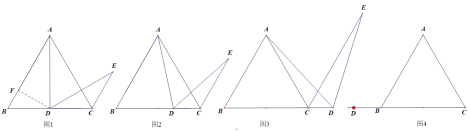
(1)如图2、当D是BC上的任意一点时,求证:![]()
(2)如图3、当D在BC的延长线上时,求证:![]()
(3)当![]() 在
在![]() 的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中![]() 表示小强从家出发后的时间,
表示小强从家出发后的时间,![]() 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量![]() 与
与![]() 之间关系的大致图象是( )
之间关系的大致图象是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家到梧州市一茶厂购买茶叶,购买茶叶数量为x千克(x>0),总费用为y元,现有两种购买方式.
方式一:若商家赞助厂家建设费11500元,则所购茶叶价格为130元/千克;(总费用=赞助厂家建设费+购买茶叶费)
方式二:总费用y(元)与购买茶叶数量x(千克)满足下列关系式:y=![]() .
.
请回答下面问题:
(1)写出购买方式一的y与x的函数关系式;
(2)如果购买茶叶超过150千克,说明选择哪种方式购买更省钱;
(3)甲商家采用方式一购买,乙商家采用方式二购买,两商家共购买茶叶400千克,总费用共计74600元,求乙商家购买茶叶多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠C=90°,∠BAC=60°,AB的垂直平分线DE交AB于D,交BC于E,若CE=3cm,则BE的长为( )

A.6cm B.5cm C.4cm D.3cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com