
科目:初中数学 来源: 题型:
| A、为了了解某品牌手机的屏幕是否耐摔,选择全面调查 |
| B、为了了解玉兔号月球车的零部件质量,选择抽样调查 |
| C、为了了解南开步行街平均每天的人流量,选择抽样调查 |
| D、为了了解中秋节期间重庆市场上的月饼质量,选择全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 5 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
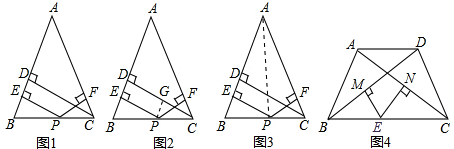
 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是30,则这个风车的外围周长是
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是30,则这个风车的外围周长是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、x2+x+12=-2+12 | ||||
| B、x2+x+22=-2+22 | ||||
C、x2+x+
| ||||
| D、x2+x+9=-2+9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com