
����Ŀ���ڡ�ABC�У���BAC��90�㣬AB��AC��DΪֱ��BC��һ����(��D����B��C�غ�) ����ADΪ����������ADEF������CF��
��1����ͼ�٣�����D���߶�BC��ʱ����֤����BD��CF����CF��BCCD��
��2����ͼ�ڣ�����D���߶�BC���ӳ�����ʱ�������������䣬��ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
��3����ͼ�ۣ�����D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣺����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ���������������ζԽ���AE��DF,����ΪO������OC��̽����AOC����״����˵�����ɣ�
���𰸡�
��1��
֤��������ͼ�٣�
�ߡ�BAC=90�㣬AB=AC��
���ACB=��ABC=45�㣬
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAD=90��-��DAC����CAF=90��-��DAC��
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
|
���BAD�ա�CAF��SAS����
���ACF=��ABD=45�㣬
���BCF=90�㣬
��BD��CF.
���ɢٵá�BAD�ա�CAF��
��BD=CF
��BD+CD=BC��
��CF=BC-CD.
��
��
��
��
��
��
��2��
�⣺CF-CD=BC���������£�
��ͼ�ڣ�
�ߡ�BAD=90��+��CAD��
��CAF=90��+��CAD��
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
|
���BAD�ա�CAF��SAS����
��BD=CF��
��BD=BC+CD��
��CF-CD=BC��
��
��
��
��
��
��
��3��
�⣺��CD-CF=BC;
�ڵ���������.�������£�
�ߡ�BAC=90�㣬��ABC=45�㣬
���ACB=��ABC=45�㣬
��AB=AC��
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAD=90��-��BAF����CAF=90��-��BAF��
���BAD=��CAF��
���ڡ�BAD�͡�CAF�У�
|
���BAD�ա�CAF��SAS����
���ACF=��ABD��
�ߡ�ABC=45�㣬
���ABD=135�㣬
���ACF=��ABD=135�㣬
���FCD=90�㣬
���FCD��ֱ�������Σ�
�֡�OD=OF��
��OC=OD=OA��
���AOC�ǵ���������.
��
��
��
��
��
��
����������1������2���ͣ�3����ÿ�ⶼҪ���á�SAS��֤����BAD�ա�CAF��Ȼ��õ��ߵĹ�ϵ�ͽǵĹ�ϵ����3���Ģڻ�Ҫ���õ�ֱ����������б���ϵ�������б�߳���һ��.
�����㾫�������õ���ֱ�������κ�ֱ��������б���ϵ����߶���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=6��AE��BD������ΪE��ED=3BE����P��Q�ֱ���BD��AD�ϣ���AP+PQ����СֵΪ�� ��
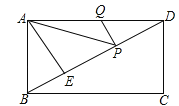
A��![]() B��
B��![]() C��
C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�⣺��ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С�����εĶ��������㣮��AOB����������A��O��B���ڸ���ϣ�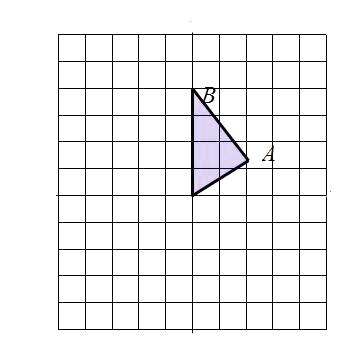
��1��������AOB���ڵ�O�����ĶԳƵ������Σ�
��2��������AOB�Ƶ�O��ʱ����ת90��õ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��9������ ![]() ��2+
��2+ ![]() ��|��3|
��|��3|
��2��![]()
��3��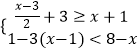
����������ʽ��Ľ⼯�����������ϱ�ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У�AC��BD��˳���������ĸ����е����õ��ı�����_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F��
��1��PC=PE��
��2�����CPE�Ķ�����
��3����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ������CE����̽���߶�AP���߶�CE��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ַ���ԭ���ۼ�ÿ��2Ԫ��������2�����ϣ�����2����,�̳��Ƴ������Ż����۰취.��һ�֣�һ�������ԭ�ۣ����ఴԭ�۵��������ۣ��ڶ��֣�ȫ����ԭ�۵İ�������.���ڹ�����ͬ��������������£�Ҫʹ��һ�ַ����ȵڶ��ַ����õ����Żݶ࣬������Ҫ�� �������.
A. 5 B. 4 C. 3 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
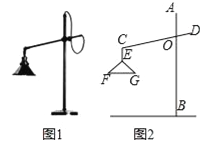
����Ŀ����ͼ1��ʾ����һ�����������ϵļ���̨�ƣ�����ṹ��ͼ2���Ƹ�AB��CD���ڵ�O����O�̶�������������CEʼ�ձ�����ABƽ�У������·�FG����ˮƽλ�ã����OC=20cm����COB=70�㣬��F=40�㣬EF=EG����G��OB�ľ���Ϊ12cm��
��1������CEG�Ķ�����
��2������ֵĿ��ȣ�FG�ij��������ȷ��0.1cm�����ÿ�ѧ����������
���ο����ݣ�sin40����0.643��cos40����0.766��sin70����0.940��cos70����0.342��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com