
【题目】如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,求证:△PDH的周长是定值;
(3)当BE+CF的长取最小值时,求AP的长.

【答案】(1)见解析;(2)△PDH的周长是定值为8,理由见解析;(3)2
【解析】试题分析:(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;
(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;
(3)过F作FM⊥AB,垂足为M,则FM=BC=AB,证明△EFM≌△BPA,设AP=x,利用折叠的性质和勾股定理的知识用x表示出BE和CF,结合二次函数的性质求出最值.
试题解析:(1)解:如图1,

∵PE=BE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)证明:如图2,过B作BQ⊥PH,垂足为Q.

由(1)知∠APB=∠BPH,
又∵∠A=∠BQP=90°,BP=BP,
在△ABP和△QBP中,
 ,
,
∴△ABP≌△QBP(AAS),
∴AP=QP,AB=BQ,
又∵AB=BC,
∴BC=BQ.
又∠C=∠BQH=90°,BH=BH,
在△BCH和△BQH中,
 ,
,
∴△BCH≌△BQH(SAS),
∴CH=QH.
∴△PHD的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
∴△PDH的周长是定值.
(3)解:如图3,过F作FM⊥AB,垂足为M,则FM=BC=AB.

又∵EF为折痕,
∴EF⊥BP.
∴∠EFM+∠MEF=∠ABP+∠BEF=90°,
∴∠EFM=∠ABP.
又∵∠A=∠EMF=90°,
在△EFM和△BPA中,
 ,
,
∴△EFM≌△BPA(AAS).
∴EM=AP.
设AP=x
在Rt△APE中,(4-BE)2+x2=BE2.
解得BE=2+![]() ,
,
∴CF=BE-EM=2+![]() -x,
-x,
∴BE+CF=![]() -x+4=
-x+4=![]() (x-2)2+3.
(x-2)2+3.
当x=2时,BE+CF取最小值,
∴AP=2.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC和射线BD上一点P(点P与点B不重合,且点P到BA,BC的距离分别为PE,PF).

(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β,请判断PE,PF的大小,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
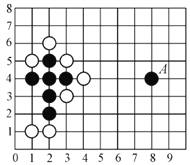
【题目】五子连珠棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记作(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面调查中,最适宜全面调查的是( )
A. 企业招聘,对应聘人员进行面试
B. 调查春节联欢晚会的收视率
C. 某批次汽车的抗撞击能力
D. 调查一批灯泡的使用寿命
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 积比每个因数都大
B. 异号两数相乘时,若负因数的绝对值较小,则积为正
C. 两数相乘,若积为正数,则这两个数一定是正数
D. 几个不等于零的数相乘时,如果有奇数个负数,那么积为负
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校购买一批办公用品,有甲、乙两家超市可供选择:甲超市给予每件0.8元的优惠价格,乙商超市的优惠条件如图象所示.

(1)分别求出在两家超市购买费用 y(元)与购买数量x(件)的函数关系式;
(2)若你是学校采购员,应如何选择才能更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com