
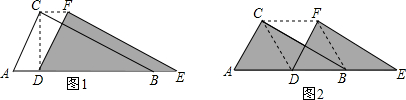
分析 (1)过点C作CG⊥AE,垂足是点G,易证四边形CDBF是梯形,在直角△ACG中利用三角形的性质求得CG,然后利用梯形的面积公式求解;
(2)首先证明四边形CDBF是平行四边形,然后根据菱形的定义即可证得四边形CDBF是菱形.
解答  解:(1)过点C作CG⊥AE,垂足是点G.
解:(1)过点C作CG⊥AE,垂足是点G.
由题可知,CF∥AE,CF=AD=BE,
则四边形CDBF是梯形.
∵在直角△ABC中,∠ACB=90°,∠A=60°,AC=1,
∴AB=2,
在直角△ACG中,∠CGA=90°,∠A=60°,AC=1,
∴∠ACG=30°,AG=$\frac{1}{2}$,
∴CG=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
∴S梯形CDBF=$\frac{1}{2}$(CE+DB)•CG=$\frac{1}{2}$(AD+DB)•CG=$\frac{1}{2}$AB•CG=$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$;
(2)四边形CDBF是菱形.
理由如下:∵在直角△ABC中,D是AB的中点,
∴AD=DB=CD,
由(1)CF=AD,
∴CF=DB=CD,
又∵CF∥AE,
∴四边形CDBF是平行四边形.
∵CD=BD,
∴四边形CDBF是菱形.
点评 本题考查了梯形和菱形的判定,正确作出辅助线,证明四边形CDBF是平行四边形是关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
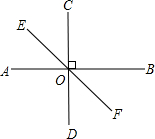 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )| A. | 30° | B. | 40° | ||
| C. | 50° | D. | 以上结果均不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
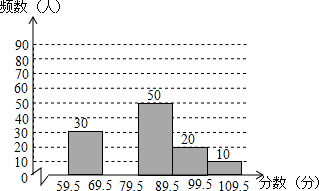 某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:
某中学举行了一次“生活中的”知识竞赛,赛后李老师抽取部分参赛同学的成绩(成绩为整数,满分为110分).进行整理,并制成图表(不完整)如下:| 分数段 | 频数 | 频率 |
| 第一次:59.5-69.5 | 30 | 0.15 |
| 第二次:69.5-79.5 | 90 | 0.45 |
| 第三次79.5-89.5 | 50 | 0.25 |
| 第四组89.5-99.5 | 20 | 0.1 |
| 第五组99.5-109.5 | 10 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
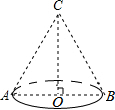 如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )| A. | 30cm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 120cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
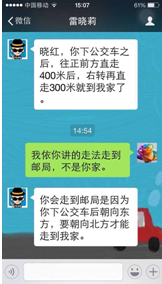 如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )| A. | 向北直走700米,再向西直走100米 | B. | 向北直走100米,再向东直走700米 | ||
| C. | 向北直走300米,再向西直走400米 | D. | 向北直走400米,再向东直走300米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com