
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论: ①c>0; ②4a-2b+c>0. ③2a-b=0;④若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1>y2; 其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
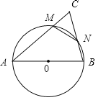
【题目】如图,以![]() 的边
的边![]() 为直径画圆,与边
为直径画圆,与边![]() 交于
交于![]() ,与边
,与边![]() 交于
交于![]() ,已知
,已知![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,
倍,![]() 中有一个内角度数是另一内角度数的
中有一个内角度数是另一内角度数的![]() 倍,试计算
倍,试计算![]() 三个内角的度数:________.
三个内角的度数:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有![]() 、
、![]() 两种商品,
两种商品,![]() 商品每件售价
商品每件售价![]() 元,
元,![]() 商品每件售价
商品每件售价![]() 元,
元,![]() 商品每件的成本是
商品每件的成本是![]() 元.
元.
根据市场调查“若按上述售价销售,该商场每天可以销售![]() 商品
商品![]() 件,若销售单价毎上涨
件,若销售单价毎上涨![]() 元,
元,![]() 商品每天的销售量就减少
商品每天的销售量就减少![]() 件.
件.
![]() 请写出
请写出![]() 商品每天的销售利润
商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() 元之间的函数关系?
元之间的函数关系?
![]() 当销售单价为多少元时,
当销售单价为多少元时,![]() 商品每天的销售利润最大,最大利润是多少?
商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
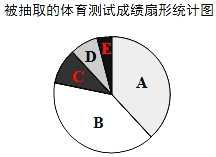
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级(5)班的学生到野外进行数学活动,为了测量一池塘两端A、B之间的距离,同学们设计了如下两种方案:
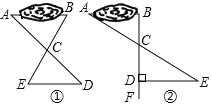
方案1:如图(1),先在平地上取一个可以直接到达A、B的点C,连接AC并延长AC至点D,连接BC并延长至点E,使DC=AC,EC=BC,最后量出DE的距离就是AB的长.
方案2:如图(2),过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB间的距离
问:(1)方案1是否可行?并说明理由;
(2)方案2是否可行?并说明理由;
(3)小明说:“在方案2中,并不一定需要BF⊥AB,DE⊥BF,将“BF⊥AB,DE⊥BF”换成条 也可以.”你认为小明的说法正确吗?如果正确的话,请你把小明所说的条件补上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南湖生态城某楼盘准备以每平方米![]() 元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米![]() 元的均价开盘销售.
元的均价开盘销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 王先生准备以开盘价均价购买一套
王先生准备以开盘价均价购买一套![]() 平方米的住房,开发商给予以下两种优惠方案:
平方米的住房,开发商给予以下两种优惠方案:
①打![]() 折销售;
折销售;
②不打折,一次性送装修费每平方米![]() 元,试问那种方案更优惠?
元,试问那种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com