
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一动点,点
边上的一动点,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数
的度数
(3)若![]() ,求
,求![]() 的值.
的值.
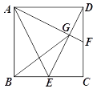
【答案】(1)见解析;(2)∠AGD=90°;(3)![]() .
.
【解析】
(1)直接利用正方形的性质得到AD=DC,∠ADF=∠DCE,![]() ,结合全等三角形的判定方法得出答案;
,结合全等三角形的判定方法得出答案;
(2)根据∠DAF=∠CDE和余角的性质可得∠AGD=90°;
(3)利用全等三角形的判定和性质得出△ABH≌△ADG(AAS),即可得出![]() 的值.
的值.
(1)证明:∵四边形ABCD是正方形,
∴AD=DC,∠ADF=∠DCE=90°,
在△ADF和△DCE中
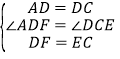 ;
;
∴△ADF≌△DCE(SAS);
(2)解:由(1)得△ADF≌△DCE,
∴∠DAF=∠CDE,
∵∠ADG+∠CDE=90°,
∴∠ADG+∠DAF=90°,
∴∠AGD=90°,
(3)过点B作BH⊥AG于H
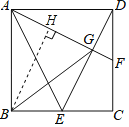
∵BH⊥AG,
∴∠BHA=90°,
∴∠BHA=∠AGD,
∵四边形ABCD是正方形,
∴AB=AD=BC,∠BAD=90°,
∵∠ABH+∠BAH=90°,∠DAG+∠BAH=90°,
∴∠ABH=∠DAG,
在△ABH和△ADG中
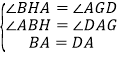 ,
,
∴△ABH≌△ADG(AAS),
∴AH=DG,
∵BG=BC,BA=BC,
∴BA=BG,
∴AH=![]() AG,
AG,
∴DG=![]() AG,
AG,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.
已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:(A组:x<155;B组:155≤x<160;C组:160≤x<165;D组165≤x<170;E组:x≥170)
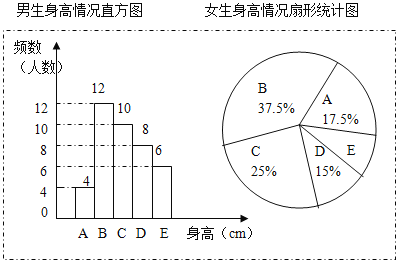
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组.
(2)样本中,女生的身高在E组的人数有 人.
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 过点
过点![]() ,直线
,直线![]() :
:![]() 与直线
与直线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
① 当b=4时,直接写出△OBC内的整点个数;
②若△OBC内的整点个数恰有4个,结合图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,已知数
,已知数![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数 表示的点重合;
与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() 、
、![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示);
的式子表示);
(4)在(3)的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
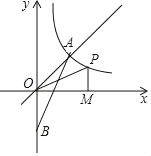
【题目】如图,点P是反比例函数y=![]() (k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(1)求反比例函数的解析式;
(2)若点B坐标为(0,﹣2),点A为直线y=x与反比例函数y=![]() (k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
(k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝商家计划平均每天销售某品牌儿童滑板车100辆,但由于种种原因,实际每天的销售量与计划量相比有出入。下表是某周的销售情况(超额记为正、不足记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
(1)根据记录的数据可知该店前三天共销售该品牌儿童滑板车______辆。
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______辆。
(3)该店实行每日计件工资制,每销售一辆车可得40元,若超额完成任务,则超过部分每辆另奖15元;少销售一辆扣20元,那么该店铺的销售人员这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
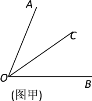
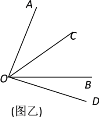
【题目】阅读下面材料:数学课上,老师给出了如下问题:如图甲,∠AOB=70°,OC平分∠AOB.
若∠BOD=20°,请你补全图形,并求∠COD的度数.
以下是小明的解答过程:
解:如图乙,因为OC平分∠AOB,∠AOB=70°,
所以∠BOC=____∠AOB=________°.
因为∠BOD=20°,
所以∠COD= °.
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部” .
完成以下问题:
(1)请你将小明的解答过程补充完整;
(2)根据小静的想法,请你在图甲中画出另一种情况对应的图形,求出此时∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D.
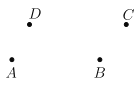
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com