【题目】如图，已知四点A、B、C、D．
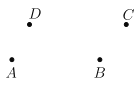
（1）用圆规和无刻度的直尺按下列要求与步骤画出图形：
①画直线AB．
②画射线DC．
③延长线段DA至点E，使
．(保留作图痕迹)
④画一点P，使点P既在直线AB上，又在线段CE上．
（2）在（1）中所画图形中，若
cm，
cm，点F为线段DE的中点，求AF的长．
科目：初中数学 来源： 题型：
【题目】已知数轴上两点A、B对应的数分别为—1，3，点P为数轴上一动点，其对应的数为x。
⑴若点P到点A、点B的距离相等，求点P对应的数；
⑵数轴上是否存在点P，使点P到点A、点B的距离之和为5？若存在，请求出x的值。若不存在，请说明理由？
⑶当点P以每分钟一个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度向左运动，点B以每分钟20个单位长度向左运动，问它们同时出发，几分钟后点P到点A、点B的距离相等？
查看答案和解析>>
科目：初中数学 来源： 题型：
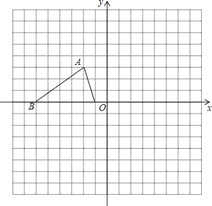
【题目】如图，△ABC的三个顶点的坐标分别为A(﹣2，3)、B(﹣6，0)、C(﹣1，0).
(1)画出把△ABC向下平移4个单位后的图形．
(2)画出将△ABC绕原点O按顺时针方向旋转90°后的图形．
(3)写出符合条件的以A、B、C、D为顶点的平行四边形的第四个顶点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
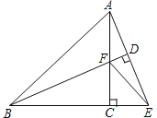
【题目】如图，在△ABC中，AC⊥BC，AC=BC，延长BC至E使BE=BA，过点B作BD⊥AE于点D，BD与AC交于点F，连接EF．
(1)求证：△ACE≌△BCF.
(2)求证：BF=2AD，
(3)若CE=
，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”
设井深为x尺，根据题意列方程，正确的是（ ）
A. 3（x+4）=4（x+1） B. 3x+4=4x+1
C. 3（x﹣4）=4（x﹣1） D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
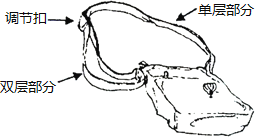
【题目】如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成．乐乐用后发现，通过调节扣加长或缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不计）增长或缩短．经测量，得到如下数据：
单层部分的长度（cm） | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度（cm） | … | 73 | 72 | 71 |
| … | 0 |
（1）根据上表中数据的规律，填写表格中空白处的数据；
（2）设单层部分的长度为xcm，请用含x的代数式表示出双层部分的长度 cm；
（3）根据乐乐的身高和习惯，挎带的长度为110cm时，背起来最舒适，请求出此时单层部分的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用同样大小的两种不同颜色的正方形纸片，按图的方式拼正方形.
(1)第①个图形中有1个小正方形，第②个图形中有4个小正方形，第③个图形中有9个小正方形，第⑦个图形中有__________个小正方形.
(2)第⑩个图形比第⑨个图形多_________个小正方形.
(3)第n个图形比第n-1个图形多_________个小正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
