
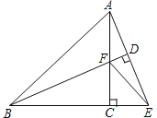
【题目】如图,在△ABC中,AC⊥BC,AC=BC,延长BC至E使BE=BA,过点B作BD⊥AE于点D,BD与AC交于点F,连接EF.
(1)求证:△ACE≌△BCF.
(2)求证:BF=2AD,
(3)若CE=![]() ,求AC的长.
,求AC的长.
【答案】(1)证明见解析;(2)证明见解析;(3)2+![]() .
.
【解析】
(1)由△ABC是等腰直角三角形,得到AC=BC,∠FCB=∠ECA=90°,由于AC⊥BE,BD⊥AE,根据垂直的定义得到∠CBF+∠CFB=90°,∠DAF+∠AFD=90°,由于∠CFB=∠AFD,于是得到∠CBF=∠CAE,证得△BCF≌△ACE;
(2)由(1)得出AE=BF,由于BE=BA,BD⊥AE,于是得到AD=ED,即AE=2AD,即可得到结论;
(3)由(1)知△BCF≌△ACE,推出CF=CE=![]() ,在Rt△CEF中,EF=
,在Rt△CEF中,EF=![]() =2,由于BD⊥AE,AD=ED,求得AF=FE=2,于是结论即可.
=2,由于BD⊥AE,AD=ED,求得AF=FE=2,于是结论即可.
(1)∵AC⊥BC,BD⊥AE
∴∠FCB=∠BDA=90°
∠CBF+∠CFB=90°,∠DAF+∠AFD=90°
∵∠CFB=∠AFD
∴∠CBF=∠CAE
∵AC=BC
∴△ACE≌△BCF
(2)由(1)知△ACE≌△BCF得AE=BF
∵BE=BA,BD⊥AE
∴AD=ED,即AE=2AD
∴BF=2AD
(3)由(1)知△ACE≌△BCF
∴CF=CE=![]()
∴在Rt△CEF中,EF=![]() =2,
=2,
∵BD⊥AE,AD=ED,
∴AF=FE=2,
∴AC=AF+CF=2+![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为4kg(在弹性限度内)时,弹簧的总长L(cm)是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
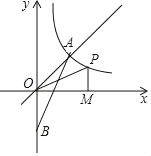
【题目】如图,点P是反比例函数y=![]() (k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(1)求反比例函数的解析式;
(2)若点B坐标为(0,﹣2),点A为直线y=x与反比例函数y=![]() (k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
(k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
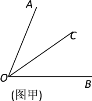
【题目】阅读下面材料:数学课上,老师给出了如下问题:如图甲,∠AOB=70°,OC平分∠AOB.
若∠BOD=20°,请你补全图形,并求∠COD的度数.
以下是小明的解答过程:
解:如图乙,因为OC平分∠AOB,∠AOB=70°,
所以∠BOC=____∠AOB=________°.
因为∠BOD=20°,
所以∠COD= °.
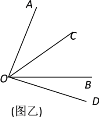
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部” .
完成以下问题:
(1)请你将小明的解答过程补充完整;
(2)根据小静的想法,请你在图甲中画出另一种情况对应的图形,求出此时∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
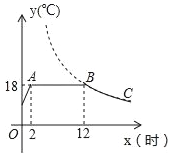
【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=15时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D.
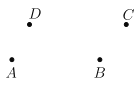
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
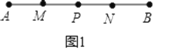
【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
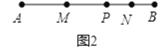
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
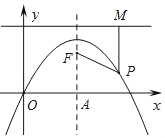
【题目】如图,抛物线y=﹣x2+2x的对称轴与x轴交于点A,点F在抛物线的对称轴上,且点F的纵坐标为![]() .过抛物线上一点P(m,n)向直线y=
.过抛物线上一点P(m,n)向直线y=![]() 作垂线,垂足为M,连结PF.
作垂线,垂足为M,连结PF.
(1)当m=2时,求证:PF=PM;
(2)当点P为抛物线上任意一点时,PF=PM是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
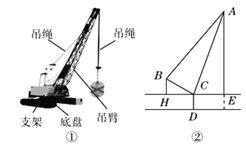
【题目】如图①,②分别是某吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角. 吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A距地面的高度是多少米?(精确到0.1米. 参考数据:sin10°=cos80°≈0.17,cos10°=sin80°≈0.98,sin20°=cos70°≈0.34,tan70°≈2.75,sin70°≈0.94)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com