
【题目】用同样大小的两种不同颜色的正方形纸片,按图的方式拼正方形.

(1)第①个图形中有1个小正方形,第②个图形中有4个小正方形,第③个图形中有9个小正方形,第⑦个图形中有__________个小正方形.
(2)第⑩个图形比第⑨个图形多_________个小正方形.
(3)第n个图形比第n-1个图形多_________个小正方形.
【答案】(1)49; (2)19; (3)2n-1
【解析】
根据已知图形得出第2个图形比第1个图形多:4-1=3个;第3个图形比第2个图形多:9-4=5个;第4个图形比第3个图形多:16-9=7个;即可得出后面一个图形比前面一个图形多的个数是连续奇数,进而得出公式第n个图形比第(n-1)个图形多2n-1个小正方形;由此利用规律得出答案即可.
解:由题意得:第2个图形比第1个图形多:4-1=3个;第3个图形比第2个图形多:9-4=5个;第4个图形比第3个图形多:16-9=7个,
∴第n个图形比第(n-1)个图形多2n-1个小正方形,
(1)第⑦个图形有:1+3+5+7+9+11+13=49个小正方形;
(2)第⑩个图形比第⑨个图形多2×10-1=19个小正方形;
(3)第n个图形比第n-1个图形多2n-1个小正方形.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,已知数
,已知数![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数 表示的点重合;
与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() 、
、![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示);
的式子表示);
(4)在(3)的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D.
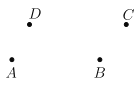
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
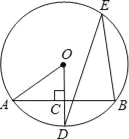
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
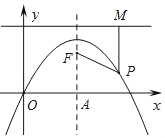
【题目】如图,抛物线y=﹣x2+2x的对称轴与x轴交于点A,点F在抛物线的对称轴上,且点F的纵坐标为![]() .过抛物线上一点P(m,n)向直线y=
.过抛物线上一点P(m,n)向直线y=![]() 作垂线,垂足为M,连结PF.
作垂线,垂足为M,连结PF.
(1)当m=2时,求证:PF=PM;
(2)当点P为抛物线上任意一点时,PF=PM是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() ,
,![]() 均为正数,且
均为正数,且![]() ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
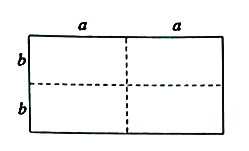
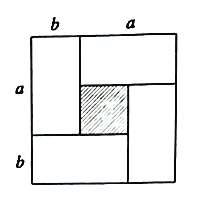
图1 图2
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:![]() 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合![]() ,
,![]() 的数值加以验证.
的数值加以验证.
(3)已知![]() .则代数式
.则代数式![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
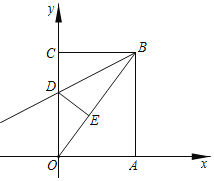
(1)求直线OB的解析式及线段OE的长;
(2)求直线BD的解析式及点E的坐标;
(3)若点P是平面内任意一点,点M是直线BD上的一个动点,过点M作![]() 轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
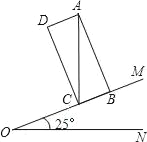
【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com