Question

【题目】(1)任意四边形四边中点围成的四边形是__________；

(2)对角线相等的四边形四边中点围成的四边形是__________；

(3)对角线垂直的四边形四边中点围成的四边形是__________；并证明．

Answer 1

【答案】平行四边形菱形矩形

【解析】

（1）连接任意四边形的中点，如图，连接AC，根据三角形的中位线定理，可以证得HG=FE=AC，并且HG∥EF，所以利用平行四边形的判定定理可知，该中点四边形是平行四边形．

（2）在（1）的基础上，易证平行四边形GHBF的一组邻边相等，所以根据菱形的定义可知该中点四边形是菱形．

（3）在（1）的基础上，易证平行四边形GHBF中有一个角是直角，所以根据矩形的定义可知该中点四边形是矩形．

（1）如图所示，任意四边形ABCD中，E、F、G、H分别为各边的中点，求四边形EFGH的形状．

连接AC，

∵E、F、G、H分别为各边的中点，

∴HG、EF分别为△ACD与△ABC的中位线，

∴HG∥AC∥EF，HG=EF=AC，

∴四边形EFGH是平行四边形；

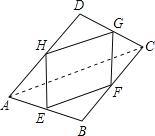
（2）如图所示，四边形ABCD的对角线AC=BD，E、F、G、H分别为各边的中点，求四边形EFGH的形状．

连接AC、BD，

∵E、F、G、H分别为各边的中点，

∴EH、GF分别为△ABD与△BCD的中位线，

∴EH∥BD∥GF，EH=GF=BD，

∴四边形EFGH是平行四边形，

同理可得，HG=EF=AC，

∵AC=BD，

∴EH=GF，

∴四边形EFGH是菱形；

（3）如图所示，四边形ABCD的对角线AC⊥BD，E、F、G、H分别为各边的中点，求四边形EFGH的形状．

解：连接AC、BD，

∵E、F、G、H分别为各边的中点，

∴EH、GF分别为△ABD与△BCD的中位线，

∴EH∥BD∥GF，EH=GF=BD，

∴四边形EFGH是平行四边形，

同理可得，HG∥AC∥EF，

∵AC⊥BD，

∴HG⊥BD⊥EH，

∴四边形EFGH是矩形．