
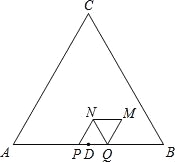
【题目】如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).
(1)当点N落在边BC上时,求t的值.
(2)当点N到点A、B的距离相等时,求t的值.
(3)当点Q沿D→B运动时,求S与t之间的函数表达式.
(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.
【答案】(1)![]() (2)2(3)S=S菱形PQMN=2S△PNQ=
(2)2(3)S=S菱形PQMN=2S△PNQ=![]() t2;
t2;![]() (4)t=1或
(4)t=1或![]()
【解析】
试题分析:(1)由题意知:当点N落在边BC上时,点Q与点B重合,此时DQ=3;
(2)当点N到点A、B的距离相等时,点N在边AB的中线上,此时PD=DQ;
(3)当0≤t≤![]() 时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当
时,四边形PQMN与△ABC重叠部分图形为四边形PQMN;当![]() ≤t≤
≤t≤![]() 时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.
时,四边形PQMN与△ABC重叠部分图形为五边形PQFEN.
(4)MN、MQ与边BC的有交点时,此时![]() <t<
<t<![]() ,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
,列出四边形PEMF与四边形PQMN的面积表达式后,即可求出t的值.
试题解析:(1)∵△PQN与△ABC都是等边三角形,
∴当点N落在边BC上时,点Q与点B重合.
∴DQ=3
∴2t=3.
∴t=![]() ;
;
(2)∵当点N到点A、B的距离相等时,点N在边AB的中线上,
∴PD=DQ,
当0<t<![]() 时,
时,
此时,PD=t,DQ=2t
∴t=2t
∴t=0(不合题意,舍去),
当![]() ≤t<3时,
≤t<3时,
此时,PD=t,DQ=6﹣2t
∴t=6﹣2t,
解得t=2;
综上所述,当点N到点A、B的距离相等时,t=2;
(3)由题意知:此时,PD=t,DQ=2t
当点M在BC边上时,
∴MN=BQ
∵PQ=MN=3t,BQ=3﹣2t
∴3t=3﹣2t
∴解得t=![]()
如图①,当0≤t≤![]() 时,
时,
S△PNQ=![]() PQ2=
PQ2=![]() t2;
t2;
∴S=S菱形PQMN=2S△PNQ=![]() t2,
t2,
如图②,当![]() ≤t≤
≤t≤![]() 时,
时,
设MN、MQ与边BC的交点分别是E、F,
∵MN=PQ=3t,NE=BQ=3﹣2t,
∴ME=MN﹣NE=PQ﹣BQ=5t﹣3,
∵△EMF是等边三角形,
∴S△EMF=ME2=
![]() (5t﹣3)2
(5t﹣3)2
![]() .
.
![]() ;
;
(4)MN、MQ与边BC的交点分别是E、F,
此时![]() <t<
<t<![]() ,
,
t=1或![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点M(a,1)在一次函数y=-x+3的图象上,则点N(2a-1,a)所在的象限是( )
A. 一象限 B. 二象限 C. 四象限 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家统计局的相关数据显示,2015年我国国民生产总值(GDP)约为67670000000000元,将67670000000000用科学记数法表示为( )
A.6.767×1013
B.6.767×1012
C.67.67×1012
D.6.767×1014
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界文化遗产长城总长约6700000m,6700000用科学记数法可表示为( )
A.6.7×105B.67×105C.6.7×106D.67×106
查看答案和解析>>
科目:初中数学 来源: 题型:
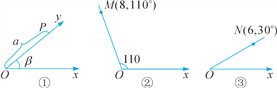
【题目】如图①,将射线Ox按逆时针方向旋转β,得到的射线Oy,如果P为射线Oy上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为(a,β).例如,图②中,如果OM=8,∠xOM=110°,那么点M在平面内的位置记为M(8,110°),根据图形,解答下列问题:
(1)如图③,如果点N在平面内的位置记为N(6,30°),那么ON=__ __,∠xON= .
(2)如果点A,B在平面内的位置分别记为A(5,30°),B(12,120°),求A,B两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下内容,并回答问题:
若一个三角形的两边平方和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是 命题(填“真”或“假”);
(2)在△ABC中,已知∠C=90°,△ABC的内角∠A、∠B、∠C所对边的长分别为a、b、c,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
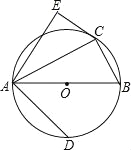
(3)如图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A、B不重合),D是半圆![]() 的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
的中点,C、D在直径AB的两侧,若存在点E,使AE=AD,CB=CE.求证:△ACE是奇异三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com