
分析 结合定义找出[t]和[-t],由a是t的小数部分,b是-t的小数部分,表示出a、b套入$\frac{1}{2b}$-$\frac{1}{a}$即可得出结论.
解答 解:t=$\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}$=2+$\sqrt{3}$,
∴[t]=3,[-t]=-4.
∵是t的小数部分,b是-t的小数部分,
∴a=2+$\sqrt{3}$-3=$\sqrt{3}$-1,b=-(2+$\sqrt{3}$)-(-4)=2-$\sqrt{3}$.
$\frac{1}{2b}$-$\frac{1}{a}$=$\frac{1}{2(2-\sqrt{3})}$-$\frac{1}{\sqrt{3}-1}$=$\frac{2+\sqrt{3}}{2(2-\sqrt{3})(2+\sqrt{3})}$-$\frac{\sqrt{3}+1}{(\sqrt{3}-1)(\sqrt{3}+1)}$=$\frac{2+\sqrt{3}}{2}$-$\frac{\sqrt{3}+1}{2}$=$\frac{1}{2}$.
点评 本题考查了估算无理数的大小,解题的关键是找出a、b.本题属于基础题,难度不大,但在运算过程中用到了使用平方差公式将分母有理化,此处需要注意别出现差错.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
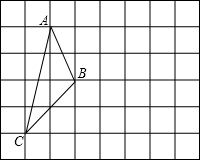 如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
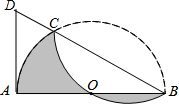 已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.
已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com