Question

【题目】在平面直角坐标系中，抛物线与轴交于点，顶点为点，点与点关于抛物线的对称轴对称．

求直线的解析式；

点在抛物线上，且点的横坐标为．将抛物线在点，之间的部分（包含点，）记为图象，若图象向下平移个单位后与直线只有一个公共点，求的取值范围．

Answer 1

【答案】(1)；(2)．

【解析】

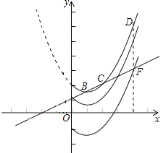
(1)欲求直线BC的解析式，需要求得点B、C的坐标，由抛物线解析式求得点A、B的坐标，然后根据点的对称性得到点C的坐标，然后由待定系数法来求直线方程；(2)根据抛物线解析式易求D(4，6)，由直线易求点(0，1)，点F(4，3)，设点A平移后的对应点为点A'，点D平移后的对应点为点D'，当图象G向下平移至点

A'与点E重合时，点D'在直线BC上方，此时t＝1，当图象G向下平移至点D'与点F重合时，点A'在直线BC下方，此时t＝3，结合图象可以知道，符合题意的t的取值范围是1＜t≤3.

∵抛物线与轴交于点，

∴点的坐标为．

∵，

∴抛物线的对称轴为直线，顶点的坐标为．

又∵点与点关于抛物线的对称轴对称，

∴点的坐标为，且点在抛物线上．

设直线的解析式为．

∵直线经过点和点，

∴，

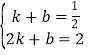解得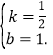

∴直线的解析式为：；

∵抛物线中，当时，，

∴点的坐标为．

∵直线中，当时，．当时，，

∴如图，点的坐标为，点的坐标为．

设点平移后的对应点为点，点平移后的对应点为点．当图象向下平移至点与点重合时，点在直线上方，

此时．

当图象向下平移至点与点重合时，点在直线下方，此时．

结合图象可知，符合题意的的取值范围是．