
【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF. 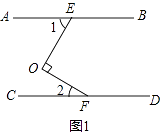
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH. 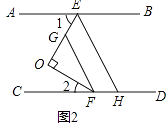
【答案】
(1)证明:过点O作OM∥AB, 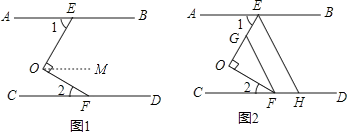
则∠1=∠EOM,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠FOM,
∵OE⊥OF,
∴∠EOF=90°,
即∠EOM+∠FOM=90°,
∴∠1+∠2=90°
(2)证明:∵AB∥CD
∴∠AEH+∠CHE=180°,
∵FO平分∠CFG,EO平分∠AEH
∴∠CFG=2∠2,∠AEH=2∠1,
∵∠1+∠2=90°
∴∠CFG+∠AEH=2∠1+2∠2=180°,
∴∠CFG=∠CHE,
∴FG∥EH
【解析】(1)过点O作OM∥AB,根据平行线的性质得出∠1=∠EOM,求出OM∥CD,根据平行线的性质得出∠2=∠FOM,即可得出答案;(2)根据平行线的性质得出∠AEH+∠CHE=180°,根据角平分线定义得出∠CFG=2∠2,∠AEH=2∠1,根据∠1+∠2=90°求出∠CFG+∠AEH=2∠1+2∠2=180°,求出∠CFG=∠CHE,根据平行线的判定得出即可.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )
A.
B.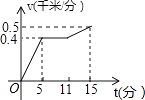
C.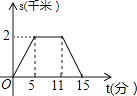
D.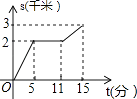
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2). 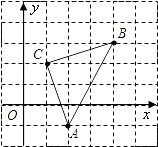
(1)写出点A、B的坐标:
A( , )、B( , )
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′( , )、B′( , )、C′( , ).
(3)△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 了解飞行员视力的达标率应使用抽样调查
B. 一组数据3,6,6,7,9的中位数是6
C. 从2000名学生中选200名学生进行抽样调查,样本容量为2000
D. 一组数据1,2,3,4,5的方差是10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2+2x-c=0中,c>0,该方程的解的情况是( ).
A.没有实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题: 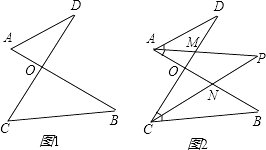
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,利用(1)的结论,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com