
【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
【答案】(1)购进A种树苗10棵,则购进B种树苗7棵 (2)当![]() 时,
时,![]() 元
元
【解析】试题分析:(1)假设购进A种树苗x棵,则购进B种树苗(17-x)棵,利用购进A、B两种树苗刚好用去1220元,结合单价,得出等式方程求解即可;(2)结合(1)的解和购买B种树苗的数量少于A种树苗的数量,可找出方案.
试题解析:
(1)设购进A种树苗x 棵,则购进B种树苗(17-x)棵,根据题意得:
80x+60(17-x )=1220,
80x+1020-60x=1220,
x =10,
∴ 17-x =7.
(2)17-x< x,
解得x >![]() ,
,
购进A、B两种树苗所需费用为80x+60(17-x)=20 x +1020,
则费用最省需x取最小整数9,此时17-x =8,这时所需费用为20×9+1020=1200(元).
答:(1)购进A种树苗10棵,B种树苗7棵;
(2)费用最省方案为:购进A种树苗9棵,B种树苗8棵. 这时所需费用为1200元.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
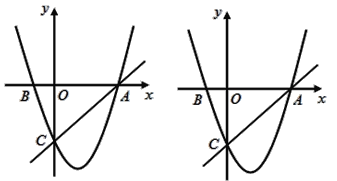
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是 ;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com