
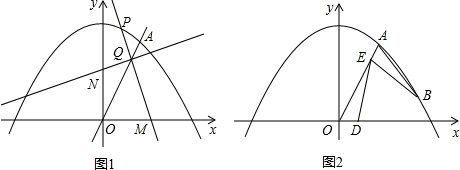
分析 (1)将已知点的坐标代入二次函数的解析式即可求得解析式;
(2)如答图1,过点Q作QG⊥y轴于点G,QH⊥x轴于点H,构造相似三角形△QHM与△QGN,将线段QM与线段QN的长度之比转化为相似三角形的相似比,即$\frac{QM}{QN}$=tan∠AOM=2为定值.需要注意讨论点的位置不同时,这个结论依然成立;
(3)由已知条件角的相等关系∠BAE=∠BED=∠AOD,可以得到△ABE∽△OED.设OE=a,则由相似边的比例关系可以得到m关于x的表达式=$\frac{1}{5}$a(3$\sqrt{5}$-a)=-$\frac{1}{5}$a2+$\frac{3\sqrt{5}}{5}$a(0<a<3$\sqrt{5}$),这是一个二次函数.借助此二次函数图象(如答图3),可见m在不同取值范围时,a的取值(即OE的长度,或E点的位置)有1个或2个.这样就将所求解的问题转化为分析二次函数的图象与性质问题.
另外,在相似三角形△ABE与△OED中,运用线段比例关系之前需要首先求出AB的长度.如答图2,可以通过构造相似三角形,或者利用一次函数(直线)的性质求得AB的长度.
解答 解:(1)∵抛物线y=ax2+c过(0,$\frac{22}{3}$),且与直线y=2x交于点A(3,6)
∴$\left\{\begin{array}{l}{c=\frac{22}{3}}\\{9a+c=6}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\frac{4}{27}}\\{c=\frac{22}{3}}\end{array}\right.$;
抛物线的解析式为:y=-$\frac{4}{27}{x}^{2}$+$\frac{22}{3}$.
(2)$\frac{QM}{QN}$是一个定值,理由如下: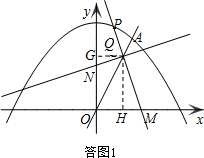
如答图1,过点Q作QG⊥y轴于点G,QH⊥x轴于点H.
①当QH与QM重合时,显然QG与QN重合,
此时$\frac{QM}{QN}$=tan∠AOM=2;
②当QH与QM不重合时,
∵QN⊥QM,QG⊥QH
不妨设点H,G分别在x、y轴的正半轴上,
∴∠MQH=∠GQN,
又∵∠QHM=∠QGN=90°
∴△QHM∽△QGN,
∴$\frac{QM}{QN}$=tan∠AOM=2,
当点P、Q在抛物线和直线上不同位置时,同理可得$\frac{QM}{QN}$=2.
(3)如答图2,延长AB交x轴于点F,过点F作FC⊥OA于点C,过点A作AR⊥x轴于点R
∵∠AOD=∠BAE,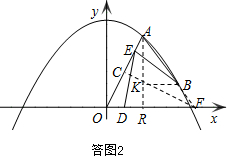
∴AF=OF,
∴OC=AC=$\frac{1}{2}$OA=$\frac{3}{2}$,
∵∠ARO=∠FCO=90°,∠AOR=∠FOC,
∴△AOR∽△FOC,
∴$\frac{OF}{OC}$=$\frac{AO}{OR}$=$\frac{3\sqrt{5}}{3}$=$\sqrt{5}$,
∴OF=$\frac{3}{2}$,
∴点F($\frac{15}{2}$,0),
设点B(x,$\frac{4}{27}{x}^{2}$+$\frac{22}{3}$),
过点B作BK⊥AR于点K,则△AKB∽△ARF,
∴$\frac{BK}{FR}$=$\frac{AK}{AR}$,
即$\frac{x-3}{7.5-3}$=-$\frac{6-(-\frac{4}{27}{x}^{2}+\frac{22}{3})}{6}$,
解得x1=6,x2=3(舍去),
∴点B(6,2),
∴BK=6-3=3,AK=6-2=4,
∴AB=5;
在△ABE与△OED中
∵∠BAE=∠BED,
∴∠ABE+∠AEB=∠DEO+∠AEB,
∴∠ABE=∠DEO,
∵∠BAE=∠EOD,
∴△ABE∽△OED.
设OE=a,则AE=3$\sqrt{5}$-a(0<a<3),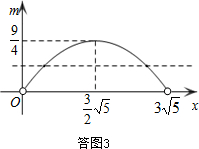
由△ABE∽△OED得$\frac{AE}{AB}$=$\frac{OD}{OE}$,
∴$\frac{3\sqrt{5}-a}{5}$=$\frac{m}{a}$,
∴m=$\frac{1}{5}$a(3$\sqrt{5}$-a)=-$\frac{1}{5}$a2+$\frac{3\sqrt{5}}{5}$a(0<a<3$\sqrt{5}$),
∴顶点为($\frac{3}{2}$,$\frac{9}{4}$)
如答图3,当m=$\frac{9}{4}$时,OE=a=$\frac{3}{2}$,此时E点有1个;
当0<m<$\frac{9}{4}$时,任取一个m的值都对应着两个a值,此时E点有2个.
∴当m=$\frac{9}{4}$时,E点只有1个
当0<m<$\frac{9}{4}$时,E点有2个.
点评 本题是中考压轴题,难度较大,解题核心是相似三角形与抛物线的相关知识,另外也考查了一次函数、勾股定理等重要知识点.解题的难点在于转化思想的运用,本题第(2),(3)问都涉及到了问题的转化,要求同学们能够将所求解的问题转化为常见的数学问题,利用自己所熟悉的数学知识去解决问题,否则解题时将不知道从何下手而导致失分.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
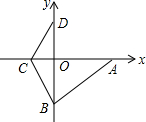 如图,在平面直角坐标系中,A点的坐标为(a,0),B点的坐标为(0,b),a,b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0,C在x轴负半轴上,且OC=$\frac{1}{2}$OB.
如图,在平面直角坐标系中,A点的坐标为(a,0),B点的坐标为(0,b),a,b满足|$\frac{1}{2}$a-4|+$\sqrt{{b}^{2}-36}$=0,C在x轴负半轴上,且OC=$\frac{1}{2}$OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com