
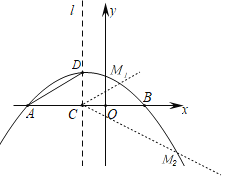
����Ŀ����ͼ��������y1��ax2+bx+![]() ��x�ύ�ڵ�A����3��0������B����D��������y1�Ķ��㣬����D��x��Ĵ��ߣ�����Ϊ��C����1��0����
��x�ύ�ڵ�A����3��0������B����D��������y1�Ķ��㣬����D��x��Ĵ��ߣ�����Ϊ��C����1��0����
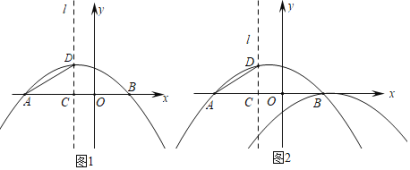
��1����������y1����Ӧ�ĺ�������ʽ��
��2����ͼ1����M��������y1�ϣ�������Ϊm������MC������MCB����DAC����m��ֵ��
��3����ͼ2����������y1ƽ�ƺ�õ�����ΪB��������y2����PΪ������y1�ϵ�һ�����㣬����P��y���ƽ���ߣ���������y2�ڵ�Q������Q��x���ƽ���ߣ���������y2�ڵ�R�����Ե�P��Q��RΪ��������������ACDȫ��ʱ����ֱ��д����P�����꣮
���𰸡���1��![]() ����2��m��ֵΪ
����2��m��ֵΪ![]() ��2+
��2+![]() ����3��P��������0��
����3��P��������0��![]() ����P��2����
����P��2����![]() ����
����
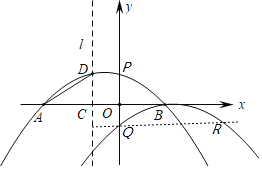
��������
(1)����A��C����������ô���ϵ�����������ʽ��
(2)��ͼ����M����x���Ϸ�ʱ������M1CB����DAC����DA��CM1������ֱ��AD�Ľ���ʽ���ɵ�C����������ֱ��CM1�Ľ���ʽ������ֱ�ߺ������߷��̿������M1�����꣬����M��x���·�ʱ������ԳƵ����ʿ����ֱ��CM2�Ľ���ʽ��ͬ������ֱ�ߺ������߷����������M�����ꣻ
(3)�����y2�Ľ���ʽ���������P���꣬��ʾQ��R���꼰PQ��QR��������P��Q��RΪ���������������ACDȫ�ȣ��������۶�Ӧ����ȵĿ����Լ�����P�����꣮
(1)������ã�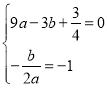 �����
�����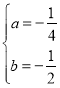 ��
��
������y1����Ӧ�ĺ�������ʽΪ![]() ��
��
(2)��x����1ʱ��y��![]() =1��
=1��
��D(��1��1)��
��ֱ��AD�Ľ���ʽΪy��kx+n��
��![]() ����ã�
����ã�![]() ��
��
��ֱ��AD�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��ͼ������M����x���Ϸ�ʱ��
�ߡ�M1CB����DAC��
��DA��CM1��
��ֱ��CM1�Ľ���ʽΪy��![]() x+b1��
x+b1��
��ֱ�߾�����C��
��-![]() +b1=0����ã�b1=
+b1=0����ã�b1=![]() ��
��
��ֱ��CM1�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��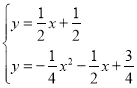 ��
��
��ã�x=-2+![]() ��x=-2-
��x=-2-![]() (��ȥ)��
(��ȥ)��
��m����2+![]() ��
��
������M��x���·�ʱ��ֱ��CM2��ֱ��CM1����x��Գƣ�
����ԳƵ����ʿɵ�ֱ��CM2�Ľ���ʽΪy��-![]() x-
x-![]() ��
��
��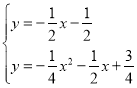 ����ã�x=
����ã�x=![]() ��x����
��x����![]() (��ȥ)��
(��ȥ)��
��m=![]() ��
��
�ۺ����Ͽɵ�m��ֵΪ![]() ��2+
��2+![]() ��
��
(3)��������y1ƽ�ƺ�õ�y2���Ҷ���ΪB(1��0)��
��![]() ��
��
��y2=![]() ��
��
��P(m��![]() )����Q(m��
)����Q(m��![]() )��
)��
��R(2��m��![]() )��
)��
����P��Q���Ϸ�ʱ��
PQ��1��m��QR��2��2m��
�ߡ�PQR����ACDȫ�ȣ�
����PQ��DC��QR��ACʱ��m��0��
��P(0��![]() )��R(2����
)��R(2����![]() )��
)��
��PQ��AC��QR��DCʱ���⣻
������P��Q���·�ʱ��
ͬ����PQ��m��1��QR��2m��2��
m��1��1��
��m��2��
��P(2��![]() )��R(0����
)��R(0����![]() )��
)��
�ۺϿɵ�P������Ϊ(0��![]() )��P(2��
)��P(2��![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�Ƴ���һ�ָ�Ч������ϴ����Ʒ,������к�,��˾�����˴ӿ���Ӯ���Ĺ���.���ù�˾��������ۻ�����s(��Ԫ)������ʱ��t(��)֮��Ĺ�ϵ(��ǰ�߸��µ������ܺ���t֮��Ĺ�ϵ)Ϊs=![]() t2-2t.
t2-2t.
(1)�ڼ�����ĩʱ,��˾�������?Ϊʲô?
(2)�ڼ�����ĩʱ,��˾�ۻ�����ɴ�30��Ԫ?
(3)���8���¹�˾���������Ƕ�����Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
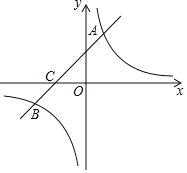
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ཻ�ڵ�һ���������ڵ�
��ͼ���ཻ�ڵ�һ���������ڵ�![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
����÷�����������һ�κ����Ľ���ʽ��
����![]() ������һ��
������һ��![]() ʹ
ʹ![]() �����
�����![]() �����ֵ����
�����ֵ����![]() �����ꣻ
�����ꣻ
��ֱ��д����![]() ʱ��
ʱ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() .��
.��![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶȣ���
����λ���ȵ��ٶȣ���![]() �����յ�
�����յ�![]() �˶�������
�˶�������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����
����![]() ���
���![]() �ڵ�
�ڵ�![]() ������
������![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��.
��.
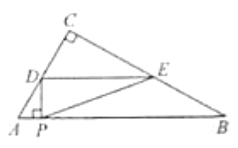
��1������![]() ��
��![]() ����ʱ��
����ʱ��![]() �ij�Ϊ________���ú�
�ij�Ϊ________���ú�![]() �Ĵ���ʽ��ʾ ��
�Ĵ���ʽ��ʾ ��
��2������![]() ΪAC�ߵ��е�ʱ����
ΪAC�ߵ��е�ʱ����![]() ��ֵ.
��ֵ.
��3����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.
��4������![]() ��
��![]() �ıߴ�ֱʱ��ֱ��д��
�ıߴ�ֱʱ��ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l��y��x+1��y�ύ�ڵ�A����˫����![]() ��x��0�����ڵ�B��2��a����
��x��0�����ڵ�B��2��a����
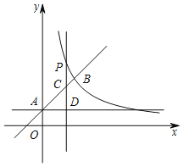
��1����a��k��ֵ��
��2����P��ֱ��l�Ϸ���˫������һ�㣬����P��ƽ����y���ֱ�ߣ���ֱ��l�ڵ�C������A��ƽ����x���ֱ�ߣ���ֱ��PC�ڵ�D�����P�ĺ�����Ϊm��
����m��![]() �����ж��߶�CP��CD��������ϵ����˵�����ɣ�����CP��CD�����Ϻ���ͼ��ֱ��д��m��ȡֵ��Χ��
�����ж��߶�CP��CD��������ϵ����˵�����ɣ�����CP��CD�����Ϻ���ͼ��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
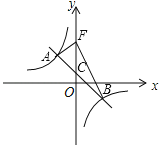
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y����x+b��ͼ���뷴��������y��![]() (k��0)��ͼ����A��B�㣬��y�ύ�ڵ�C�����е�A�İ��Ϊ(��2��3)
(k��0)��ͼ����A��B�㣬��y�ύ�ڵ�C�����е�A�İ��Ϊ(��2��3)
(1)��һ�κ����ͷ����������Ľ���ʽ��
(2)��ͼ��������C��y������ƽ��4����λ��������F������AF��BF�����ABF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��a��0��ͼ����ͼ�����н��ۣ��� abc��0���� 2a��b��0���� ��m��1ʱ��a��b��am2��bm���� a��b��c��0������ax12��bx1��ax22��bx2����x1��x2��x1��x2��2��
������ȷ���У�������

A. �٢ڢ� B. �ڢ� C. �ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����״��ͼ�����������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .Ҫ����������н�ȡһ����β��ϣ�����һ����
.Ҫ����������н�ȡһ����β��ϣ�����һ����![]() �ϣ���ʹ���ؾ��ε���������ܴ�.
�ϣ���ʹ���ؾ��ε���������ܴ�.
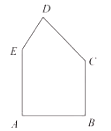
��1�������ؾ��β��ϵ�һ������![]() ��
��![]() ������β��ϵ������
������β��ϵ������
��2���ܷ�س��ȣ�1�����������ľ��β��ϣ�����ܣ������Щ���β�����������ֵ��������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��֯�н�֪ʶ��������С��ȥ����A��B����Ʒ�Ƶĸֱ���Ϊ��Ʒ����֪һ֧AƷ�Ƹֱʵļ۸��һ֧BƷ�Ƹֱʵļ۸��5Ԫ������100ԪAƷ�Ƹֱ�����50ԪBƷ�Ƹֱ���Ŀ��ͬ��
��1����A��B����Ʒ�Ƹֱʵĵ��۷ֱ�Ϊ����Ԫ��
��2�����ݻ���轱�������������A��B����Ʒ�Ƶĸֱʹ�100֧������蹺��AƷ�Ƹֱʵ�����Ϊn֧������������Ʒ�Ƶĸֱʹ�����yԪ��
��ֱ��д��y��Ԫ������n��֧���ĺ�����ϵʽ��
�����������AƷ�Ƹֱʵ�����������BƷ�Ƹֱ�������![]() ���������С��������ι�����ʹ�����ѵ�Ǯ���٣���ʱ�����Ƕ��٣�
���������С��������ι�����ʹ�����ѵ�Ǯ���٣���ʱ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com