
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度,沿
个单位长度的速度,沿![]() 边向终点
边向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,连结
,连结![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
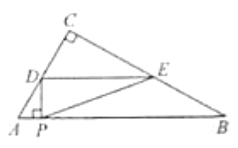
(1)当点![]() 在
在![]() 边上时,
边上时,![]() 的长为________(用含
的长为________(用含![]() 的代数式表示 )
的代数式表示 )
(2)当点![]() 为AC边的中点时,求
为AC边的中点时,求![]() 的值.
的值.
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当边![]() 与
与![]() 的边垂直时,直接写出
的边垂直时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当0<t<1时,
;(3)当0<t<1时,![]() ; 当1<t<4时,
; 当1<t<4时,![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)直接利用tan∠A进行计算即可;(2)先求出AC,进而求出AD,再利用直角三角形ADP求出AP即可;(3)分出情况,当D点在AC上与D点在BC上,利用相似三角形求出线段长,然后利用三角形面积进行解题即可(4)同样分出情况,当PE垂直AC或者PE垂直BC时的情况,然后利用三角形相似可直接解出t
(1)∠A=60°,tan∠A=tan60°=![]() =
=![]() ,得到DP=
,得到DP=![]()
(2)∠A=60°,AB=4,得到AC=2
当D为AC中点时,AD=1,在直角三角形ADP中,∠ADP=30°,所以AP=![]()
(3)当t=1时,D点与C点重合,
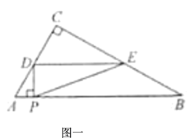
①当0<t<1时,如图一,由第一问得到DP=![]() ,DA=2t,AC=2,AB=4,DC=2-2t,
,DA=2t,AC=2,AB=4,DC=2-2t,
∵ED∥AB
∴△DCE∽△ACB
∴![]() 即
即![]()
∴DE=4-4t
∴S△PDE=![]() DE·DP 即
DE·DP 即![]()
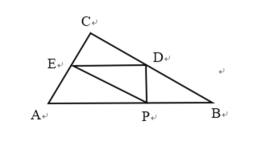
当1<t<4时,如图二BC=2![]() AP=t,BP=4-t,BD=
AP=t,BP=4-t,BD=![]() =
=![]() (4-t),CD=BC-BD=
(4-t),CD=BC-BD=![]() (t-1),因为ED∥AB,有△DCE∽△BCA,得到
(t-1),因为ED∥AB,有△DCE∽△BCA,得到![]() ,即
,即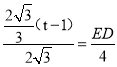 ,解出ED=
,解出ED=![]() (t-1)
(t-1)
S△PDE=![]() DE·DP 即
DE·DP 即![]()
(4)![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 了解“贵港市初中生每天课外阅读书籍时间的情况“最适合的调查方式是全面调查
B. 甲乙两人跳绳各10次,其成绩的平均数相等,若![]() 则甲的成绩比乙的稳定
则甲的成绩比乙的稳定
C. 平分弦的直径垂直于弦
D. “任意画一个三角形,其内角和是360°”是不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB——BC——CD所示(不包括端点A).
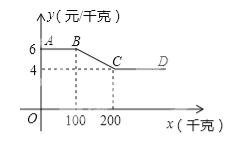
(1)当100<x<200时,直接写y与x之间的函数关系式.
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
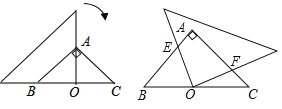
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,一个三角尺的直角顶点与
,一个三角尺的直角顶点与![]() 边的中点
边的中点![]() 重合,且两条直角边分别经过点
重合,且两条直角边分别经过点![]() 和点
和点![]() ,将三角尺绕点
,将三角尺绕点![]() 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与
按顺时针方向旋转任意一个锐角,当三角尺的两直角边与![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() 时,下列结论中错误的是( )
时,下列结论中错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
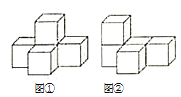
A. 主视图,俯视较和左视图都改变
B. 左视图
C. 俯视图
D. 主视图
查看答案和解析>>
科目:初中数学 来源: 题型:
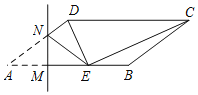
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
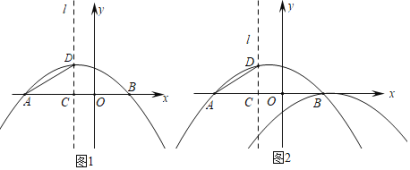
【题目】如图,抛物线y1=ax2+bx+![]() 与x轴交于点A(﹣3,0),点B,点D是抛物线y1的顶点,过点D作x轴的垂线,垂足为点C(﹣1,0).
与x轴交于点A(﹣3,0),点B,点D是抛物线y1的顶点,过点D作x轴的垂线,垂足为点C(﹣1,0).
(1)求抛物线y1所对应的函数解析式;
(2)如图1,点M在抛物线y1上,横坐标为m,连接MC,若∠MCB=∠DAC,求m的值;
(3)如图2,将抛物线y1平移后得到顶点为B的抛物线y2.点P为抛物线y1上的一个动点,过点P作y轴的平行线,交抛物线y2于点Q,过点Q作x轴的平行线,交抛物线y2于点R.当以点P,Q,R为顶点的三角形与△ACD全等时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,将边
轴上,将边![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 的点
的点![]() 处.已知折叠
处.已知折叠![]() ,且
,且![]() .
.
(1)判断![]() 与
与![]() 是否相似?请说明理由;
是否相似?请说明理由;
(2)求直线![]() 与
与![]() 轴交点
轴交点![]() 的坐标;
的坐标;
(3)是否存在过点![]() 的直线
的直线![]() ,使直线
,使直线![]() 、直线
、直线![]() 与
与![]() 轴所围成的三角形和直线
轴所围成的三角形和直线![]() 、直线
、直线![]() 与
与![]() 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.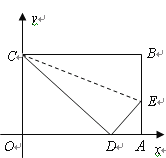
查看答案和解析>>
科目:初中数学 来源: 题型:
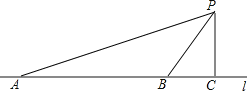
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com