
| A. | -$\frac{1}{4}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 首先把多项式利用完全平方公式变为-(x+$\frac{1}{4}$)2+$\frac{5}{16}$的形式,进一步利用非负数的性质解决问题.
解答 解:-x2-$\frac{1}{2}x$+$\frac{1}{4}$=-(x+$\frac{1}{4}$)2+$\frac{5}{16}$,
∵-(x+$\frac{1}{4}$)2≤0,
∴-(x+$\frac{1}{4}$)2+$\frac{5}{16}$≥$\frac{5}{16}$,
∴当x=-$\frac{1}{4}$时,多项式-x2-$\frac{1}{2}x$+$\frac{1}{4}$取得最大值.
故选:A.
点评 本题考查了配方法的应用,非负数的性质,根据式子的特点,灵活运用公式解决问题.


科目:初中数学 来源: 题型:解答题
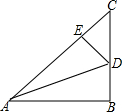 如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处.
如图,在△ABC中,∠B=90°,AB=BC=4,点D在BC上,将△ABC沿AD折叠,使点B落在AC边上的点E处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某地区随机抽查了一部分市民进行法律知识测试,测试成绩(得分取整数,每组数据含最小值不含最大值)整理后,得到如图所示的频数分布直方图,写出一条你从图中所获得的信息:分数在70~80之间的人数最多;成绩低于60分的有3人;成绩90分及其以上的有6人;参加测试的共有48人等.
某地区随机抽查了一部分市民进行法律知识测试,测试成绩(得分取整数,每组数据含最小值不含最大值)整理后,得到如图所示的频数分布直方图,写出一条你从图中所获得的信息:分数在70~80之间的人数最多;成绩低于60分的有3人;成绩90分及其以上的有6人;参加测试的共有48人等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
如图,?ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△COD,这个条件是( )
如图,线段AC与BD交于点O,且OA=OC,请添加一个条件,使△OAB≌△COD,这个条件是( )| A. | AC=BD | B. | OD=OC | C. | ∠A=∠C | D. | OA=OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com