
【题目】有以下六个命题,①同旁内角互补;②若x2=4,则x=2;③![]() ;④平分弦的直径垂直于弦;⑤等弧所对的圆心角相等;⑥相等的圆心角所对的弧相等.从这六个命题中随机任意抽取一个命题是真命题的概率为_____.
;④平分弦的直径垂直于弦;⑤等弧所对的圆心角相等;⑥相等的圆心角所对的弧相等.从这六个命题中随机任意抽取一个命题是真命题的概率为_____.
科目:初中数学 来源: 题型:
【题目】如图, 在东西方向的海岸线MN上有A,B两港口,海上有一座小岛P,渔民每天都乘轮船从A,B 两港口沿AP,BP的路线去小岛捕鱼作业.已知小岛P在A港的北偏东60°方向,在B港的北偏西45°方向,小岛P距海岸线MN的距离为30海里.
(1)求AP,BP的长(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2);
≈2.2);
(2)甲、乙两船分别从A,B两港口同时出发去小岛P捕鱼作业,甲船比乙船晚到小岛24分钟.已知甲船速度是乙船速度的1.2倍,利用(1)中的结果求甲、乙两船的速度各是多少海里/时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+4分别交x轴、y轴于A、C两点,抛物线y=﹣x2+mx+4经过点A,且与x轴的另一个交点为点B.连接BC,过点C作CD∥x轴交抛物线于点D

(1)求抛物线的函数表达式;
(2)若点E是抛物线上的点,求满足∠ECD=∠BCO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点P为第一象限内的抛物线上一点,若以点C、M、N、P为顶点的四边形是菱形,求菱形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
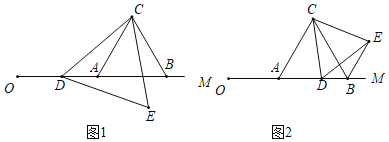
【题目】已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE,设OD=m.
(1)问题发现
如图1,△CDE的形状是 三角形.
(2)探究证明
如图2,当6<m<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.
(3)解决问题
是否存在m的值,使△DEB是直角三角形?若存在,请直接写出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
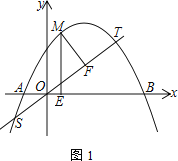
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
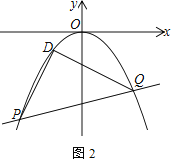
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
一、问题情境
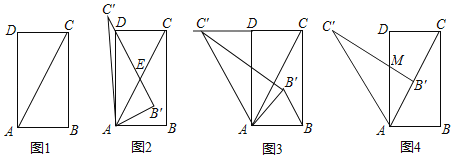
在综合与实践课上,老师组织同学们以“直角三角形的旋转”为主题开展数学活动.如图1,矩形ABCD中,AD=2AB,连接AC,将△ABC绕点A旋转到某一位置,观察图形,提出问题并加以解决.
二、实践操作,解决问题
(1)如图2,慎思组的间学将图1中的△ABC以点A为旋转中心,按逆时针方向旋转,得到△A'B'C',此时B'C'过点D,则∠ADB′=____度.
(2)博学组的同学在图2的基础上继续旋转到图3,此时点C落在CD的延长线上,连接BB',该组提出下面两个问题,并请你解决该组提出的这两个问题.
①C'D和AB有何数量关系?并说明理由.
②BB'和AC'有何位置关系?并说明理由.
(3)精英组的同学在图3的基础上按逆时针方向旋转至AB'与对角线AC重合时,B'C'与AD交于点M,如图4,则S![]() :S△ABC=_____.
:S△ABC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )

A. (![]() ,0) B. (2,0) C. (
,0) B. (2,0) C. (![]() ,0) D. (3,0)
,0) D. (3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
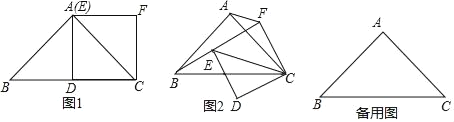
【题目】(1)(问题发现)如图1,在Rt△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,请判断线段BE与AF的数量关系并写出推断过程;
(2)(拓展研究)在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)(结论运用)在(1)(2)的条件下,若△ABC的面积为2,当正方形CDEF旋转到B,E,F三点在同一直线上时,请直接写出线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
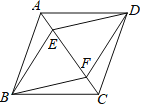
【题目】如图,在菱形ABCD中,点E、F在对角线AC上,且AE=CF,
(1)证明:△ABE≌△ADE;
(2)证明:四边形BFDE是菱形;
(3)若AC=4![]() ,BD=8,AE=
,BD=8,AE=![]() ,请求出四边形BFDE的面积.
,请求出四边形BFDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com