
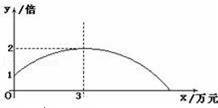
某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
| 成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
| 2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?

【考点】二次函数的应用.
【分析】(1)根据抛物线图象能够写出y与x的函数关系式,然后求出y=0时的x的值,
(2)根据利润等于销售总额减去成本费和广告费,写出函数关系式,求得最大利润.
【解答】解:(1)设y与x的函数关系式为y=a(x﹣b)2+c,
根据图象可知b=3,c=2,a=﹣
 ,
,
故y=﹣
 (x﹣3)2+2,
(x﹣3)2+2,
令y=0,解得x=7.2,
故自变量x的取值范围为0≤x<7.2,
(2)由利润等于销售总额减去成本费和广告费,可列出函数关系式
w=﹣(x﹣3)2+18﹣x,
即w=﹣x2+5x+9,
当x=2.5时,利润最大,
故投入2.5万广告费.
【点评】本题主要考查二次函数的应用,应用二次函数解决实际问题比较简单.


科目:初中数学 来源: 题型:
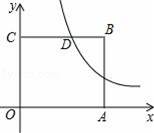
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数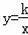
 (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
某地连续九天的最高气温统计如下表:
| 最高气温(℃) | 22 | 23 | 24 | 25 |
| 天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25 B.24.5,25 C.25,24 D.23.5,24
查看答案和解析>>
科目:初中数学 来源: 题型:
2007年中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384000千米,那么这个距离用科学记数法表示应为( )
A、3.84×104千米 B、3.84×105千米
C、3.84×106千米 D、38.4×104千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com