
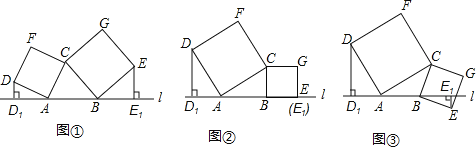
����Ŀ����ͼ����ʾ����֪A��BΪֱ��l�����㣬��CΪֱ��l�Ϸ�һ���㣬����AC��BC���ֱ���AC��BCΪ�����ABC����������CADF��������CBEG������D��DD1��l�ڵ�D1������E��EE1��l�ڵ�E1��
��1����ͼ�ڣ�����Eǡ����ֱ��l��ʱ����ʱE1��E�غϣ�����˵��DD1=AB��
��2����ͼ���У���D��E���㶼��ֱ��l���Ϸ�ʱ����̽�������߶�DD1��EE1��AB֮���������ϵ����˵�����ɣ�
��3����ͼ�ۣ�����E��ֱ��l���·�ʱ����ֱ��д�������߶�DD1��EE1��AB֮���������ϵ��������Ҫ֤����
���𰸡���1��֤�������������2��AB=DD1+EE1����3��AB=DD1-EE1��
�������������������1�����ı���CADF��CBEG�������οɵ�AD=CA����DAC=��ABC=90��������ͬ�ǵ������ȣ������ADD1=��CAB��Ȼ������AAS֤����ADD1�ա�CAB������ȫ�������εĶ�Ӧ����ȣ����ɵ�DD1=AB��
��2�����ȹ���C��CH��AB��H����DD1��AB���ɵ���DD1A=��CHA=90�������ı���CADF�������Σ��ɵ�AD=CA������ͬ�ǵ������ȣ������ADD1=��CAH��Ȼ������AAS֤����ADD1�ա�CAH������ȫ�������εĶ�Ӧ����ȣ����ɵ�DD1=AH��ͬ��EE1=BH����ɵ�AB=DD1+EE1��
��3��֤������ͬ��2�������ɵõ�AB=DD1-EE1��
�����������1����Ϊ�ı���CADF��CBEG�������Σ�
����AD=CA����DAC=��ABC=90����
������DAD1+��CAB=90����
��ΪDD1��AB��
������DD1A=��ABC=90����
������DAD1+��ADD1=90����
������ADD1=��CAB��
����ADD1����CAB��
��ADD1=��CAB����DD1A=��ABC ��AD=CA��
������ADD1�ա�CAB��
����DD1=AB��
��2��AB=DD1+EE1���������£�
����C��CH��AB��H ���루1��ͬ������ADD1�ա�CAH������DD1=AH��ͬ��EE1=BH������AB=DD1+EE1��
��3��AB=DD1-EE1���������£�
����C��CH��AB��H ���루1��ͬ������ADD1�ա�CAH������DD1=AH��ͬ��EE1=BH������AB=DD1-EE1��



 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������a��b������һ�������㣬�涨a��b=a2��|b|����2���3��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2015�����������ֵGDP��2014������10%�������ܵ�������Ӱ�죬Ԥ��2016���GDP��2015������7%����������GDPƽ��������Ϊx%����xӦ����ĵ�����ϵ�ǣ� ��
A.10%+7%=x%
B.��1+10%����1+7%��=2��1+x%��
C.��10%+7%��=2x%
D.��1+10%����1+7%��=��1+x%��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪���л�ʫ�ʲ�������������龰����ڶ̶���ʮ��֮�䣬����ţ�����Լ����˼�������࣬���㷢�����������£��Ļ���ֵ���ߣ�����ѧ���ʫ�ʸ����������е���ϵ����ʫ�У����Ծ������ľ�ʫ��ÿ�䶼������֣����Ծ������ľ�ʫ��ÿ�䶼���߸��֣���һ��ʫ�����������Ծ�������Ծ����13�ף�������ȴ��������20���֣�������ʫ�������ף������Ծ�����x�ף��������⣬���з���Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2��ͼ������ƽ��2����λ��������ƽ��1����λ�������������ߵĽ���ʽΪ�� ��
A. y=x2+4x+3 B. y=x2+4x+5 C. y=x2��4x+3 D. y=x2��4x��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и���|��2|��������2��2��������22����-24�У������ĸ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��BC�ߵ��е㣬E��F�ֱ���AD�����ӳ����ϣ�CE��BF������BE��CF��

��1����֤����BDF�ա�CDE��
��2����AB=AC����֤���ı���BFCE�����Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com